Comme une tasse de café chaude se refroidi ou qu’une glace fond si l’on attend, leur température ou leur phase (phase solide à phase liquide) changent.
Il y a donc eu un transfert de chaleur.
Le transfert de chaleur se fait du corps chaud vers le corps froid.

Il ne faut pas confondre la température et le flux de chaleur. La température traduit l'agitation des molécules alors que le flux de chaleur traduit la propagation de cette agitation.
Exemple:
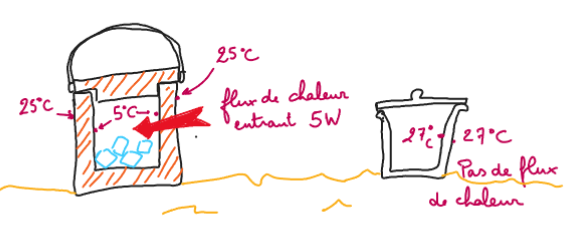
- Dans la glacière dont la température extérieure est à 25°C alors que la température intérieure est à 5°C , il y a un flux de chaleur entrant dans la glacière donné de 5 W
- dans le saut avec son couvercle les températures extérieures et intérieures sont de 27°C; il n'y a pas de flux de chaleur.
Un transfert d’énergie par chaleur peut se manifester par :
- une variation de température des systèmes concernés.
- un changement d’état physique (liquide -> solide -> gaz).
La chaleur s’écoule sous l’influence d’un gradient (variation à la hausse ou la baisse) de température par conduction des hautes vers les basses températures.
La quantité de chaleur transmise par unité de temps et par unité d’aire de la surface isotherme (même température) est appelée densité de chaleur ou flux de chaleur surfacique:
| \( \phi = {1 \over S}{{dQ} \over {dt}} \) en \( W.m^{-2} \) |
Où
- \( S \) est l’aire de la surface d'échange en m²
- \( {dQ} \over {dt} \) la variation d'énergie thermique ou chaleur du système passant à travers la surface en J/s (soit en W)
- \( \phi \) le flux de chaleur en W.m-2
On appelle flux de chaleur \( \varphi \) en W la quantité de chaleur transmise sur la globalité de la surface S par unité de temps :
| \( \varphi = {{dQ} \over {dt}} \) en \( W \) |
Un cumulus (rayon 50cm, hauteur 2m) de 400 L d'eau passe de 65°C à 60°C en 12 h.
Déterminer le flux de chaleur.
L'énergie perdue est de \( dQ = 400 \times 4185 \times (65-60) = 8,37.10^6 J \)
La puissance perdue ou flux de chaleur vaut donc \( \varphi = {{dQ} \over {dt}}= {{8,37.10^6} \over {12 \times 3600}} = 193,75 W \)
La surface extérieure du cumulus est de \( 2 \times \pi R^2 + h \times (2 \pi R) = 2\pi \times 0,5^2 + 2 \times (2 \pi \times 0,5) = 7,85 m²\)
Le flux de chaleur surfacique vaut donc \( \phi = {{\varphi} \over {S}} = {{193,75} \over {7,06}} = 24,7 W/m² \)
Physique - Echanges de chaleur 26'00:
| https://www.youtube.com/watch?v=ZJsRe0qQe4A |





