Résistance thermique d'une structure fermée (maison, appartement, armoire électrique...)
Lorsqu'on connaît la résistance thermique d'une maison, les lois de la thermique nous permettent de déterminer la relation entre écart de température intérieur et extérieur de la maison et puissance de chauffage ou de refroidissement.
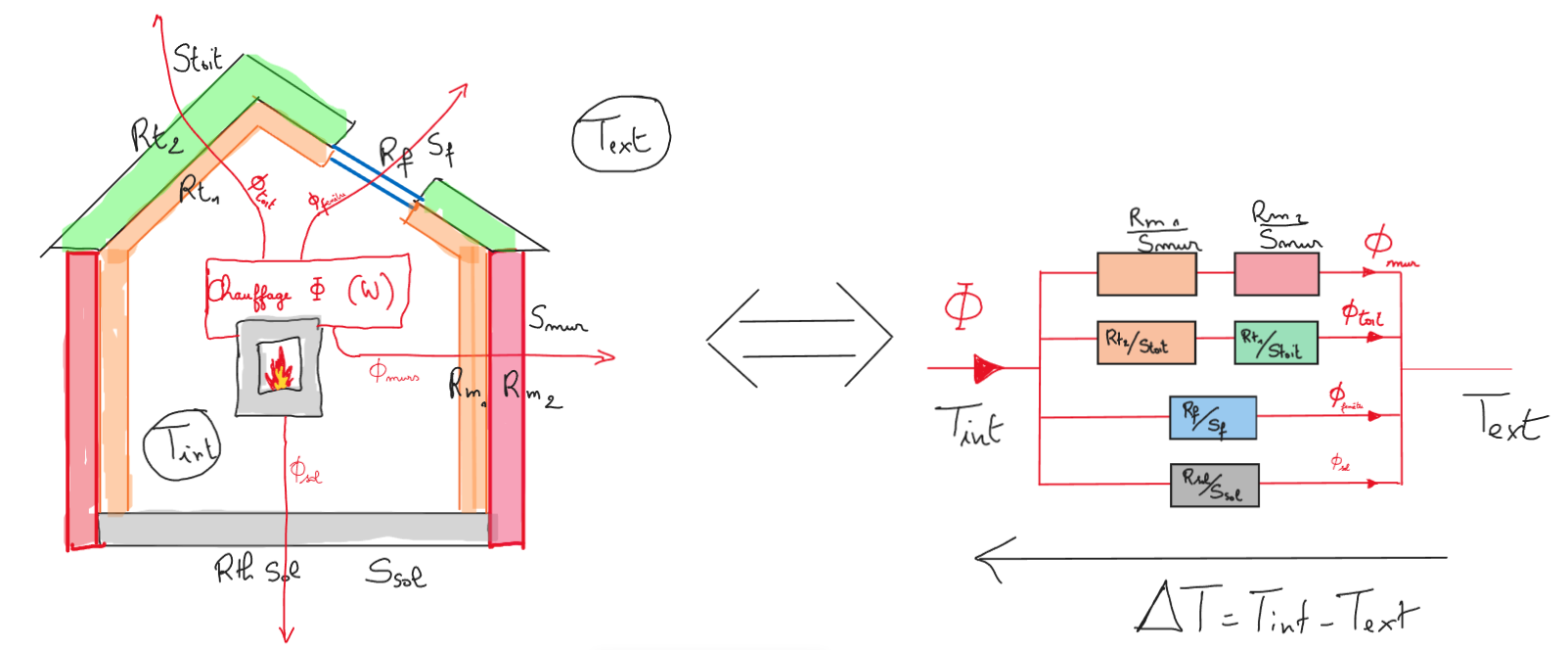
La résistance thermique globale est déterminée par la
- mise en série des résistances thermiques constituant chaque type d'enveloppe
- la mise en parallèle des résistances thermiques de chaque type d'enveloppe constituant la maison
La résistance globale \( R_{th globale} \) ainsi constituée permet de connaître les liens entre la puissance de chauffage et l'augmentation de température du système qui est tel que:
\( {R_{th}} \times \varphi = \Delta T\) ou
\( {R_{th}} \times P = (T_{int}-T{ext})\)
Mur monocouche :
Résistance thermique:
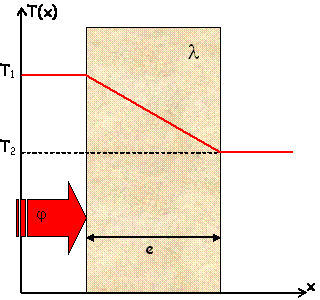
Le profil de température dans un matériau soumis à un flux de chaleur est linéaire (la température décroit doucement dans le matériau), ce que nous révèle la loi de Fourier:
\( \varphi = - \lambda S\frac{{\partial T}}{{\partial x}} \)
Donc le flux \( \varphi \) ou puissance (en W) qui passe à travers une paroi de surface S:
- est proportionnel à la conductivité thermique du matériaux \( \lambda \)
- est proportionnel à la rapidité de variation de température à travers le matériaux
Ce que l’on peut aussi mettre sous la forme: \( \varphi = \frac{{\left( {{T_1} - {T_2}} \right)}}{{\frac{e}{{\lambda S}}}} \)
On peut donc poser : \( {R_{th}} = \frac{e}{{\lambda S}} \) en \( K.W^{-1} \) qui correspond à la résistance thermique du matériau.
Analogie électrique :
Cette relation est analogue à la loi d’ohm en électricité qui définit l’intensité d’un courant comme le rapport de la différence de potentiel électrique sur la résistance électrique. La température apparaît ainsi comme un potentiel thermique et le terme \( \frac{e}{{\lambda S}} \) apparaît comme la résistance thermique d’un mur plan d’épaisseur e , de conductivité thermique \( \lambda \) et de surface S. On a donc le schéma équivalent suivant :

L’ensemble du système peut donc être modélisé ainsi :
- générateur de flux (générateur de courant )
- à travers la résistance thermique du système
- soumise à la température ambiante (tension imposée)

Résistance surfacique :
Lors de l'achat de matériaux isolant les constructeurs donnent un coefficient appelé résistance thermique mais qui est en fait une résistance thermique ramenée à 1 m².
La résistance thermique surfacique est donc définie par: \( {R_{th com}} = \frac{e}{{\lambda}} \) en \( K.W^{-1}.m^2 \)
La résistance thermique d'une paroi étant définie par \( {R_{th}} = \frac{e}{{\lambda S}} \), la résistance totale d'un mur fait d'un matériau de résistance thermique \( {R_{th com}} \) dépend donc de sa surface. Plus la surface est grande plus la résistance thermique est faible, la surface plus grande offrant plus de surface à la fuite de chaleur.
\( {R_{th}} = \frac{{R_{th com}}}{{S}} \)
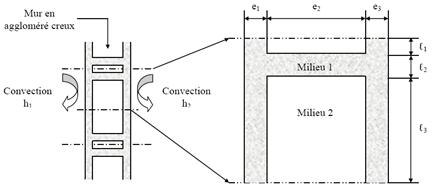
Mur multicouche :
Les résistances thermiques de convection et des diverses parties du mur s'additionnent:
\( {R_{th}} = R_{conv 1} + R_{A} + R_{B} + R_{C} + R_{conv 2} \)
soit
\( {R_{th}} = \frac{1}{h_1 S} + \frac{e_A}{\lambda_A S} + \frac{e_B}{\lambda_B S} + \frac{e_C}{\lambda_C S} + \frac{1}{h_2 S} \)
On est donc sur une association série des résistances.

Mur composite :
On est donc sur une association parallèle des résistances.
Le flux total (ou puissance perdue) est composé :
- d'un flux \( \(\varphi_1) \) qui s'échappe à travers la porte de garage . Le garage présente une résistance thermique \( R_{th1}=\frac{e_1}{\lambda_1 \times S_1} \)
- et d'un flux \( \(\varphi_2) \) qui s'échappe à travers le mur \( R_{th2}=\frac{e_2}{\lambda_2 \times S_2} \)
Ils ont soumis aux mêmes températures,

Fenêtres
Le coefficient de transmission thermique \( U \) d'une fenêtre donne le coefficient de transmission thermique en \( W.m^{-2}.K^{-1} \)
Il donne la puissance perdue par m² de surface. Donc si la surface est agrandie la puissance perdue augmente.
On peut remarquer que ce coefficient est l'inverse de la résistance thermique surfacique \( R_{th com} \): \( U = \frac{1}{R_{th com}} \)
Le flux de chaleur au travers d'une vitre est donc : \( \Phi = U \times S \times \Delta T\)
avec
- \( \Phi \) la puissance s'échappant par la fenêtre en Watt :\( W \)
- \( S \) la surface de la fenêtre en \( m^2 \)
- \( \Delta T \) l'écart de température entre l'intérieur et l'extérieur \( °C \)
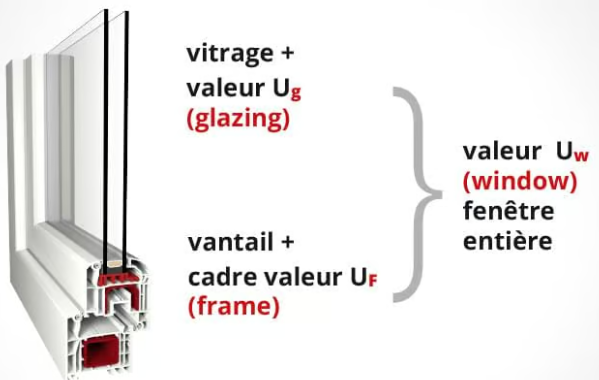
Suivant les zones de la fenêtre prise en compte on parle de coefficient
- \( U_W \) ou \( U \) \( Window \) : le coefficient UW concerne la fenêtre dans son intégralité.
- \( U_G \) ou \( U \) \( Glazing \) : le coefficient UG concerne le vitrage de la fenêtre.
- \( U_F \) ou \( U \) \( Frame \) : le coefficient UF concerne spécifiquement la performance thermique du cadre de la fenêtre.
Vidéos
Loi de Fourier et Résistance Thermique (Christophe Finot) https://www.youtube.com/watch?v=_dzP67v0B_0
Exercice utilisant la notion de résistance thermique (Christophe Finot) 3'47 https://www.youtube.com/watch?v=lZNZs78Fr3w
Physique - Puissance et échanges thermiques 10'25: https://www.youtube.com/watch?v=d6Gl3dUDDBI





