Bilan de puissance en moteur

Puissance absorbée \( P_{abs} \):
| \( {P_{abs}} = \sqrt 3 \cdot U \cdot I \cdot \cos \varphi = 3 \cdot V \cdot I \cdot \cos \varphi \) |
quelque soit le couplage
Pertes dans le stator : \( P_{jS} \)
|
Quelque soit le couplage : \( {P_{jS}} = \frac{3}{2}{R_b}{I^2} \)
|
| Couplage étoile | Couplage triangle |
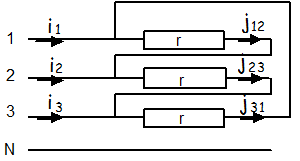
| \( {P_{jS}} = 3r{I^2} \) | \( {P_{jS}} = 3r{J^2} = r{I^2} \) |

| 
|

| 
|
|
Si on mesure la résistance entre 2 phases on mesure \( {R_b} = 2 \times r \) soit \( r = \frac{{{R_b}}}{2} \) Si on exprime \( P_{js} \) en fonction de \( R_b \) on obtient \( {P_{jS}} = 3r{I^2} = 3\frac{{{R_b}}}{2}{I^2} \) |
Si on mesure la résistance entre 2 phases on mesure \( {R_b} = \left( {2 \times r} \right)//r = \frac{{2 \times r \times r}}{{2 \times r + r}} = \frac{{2{r^2}}}{{3 \times r}} = \frac{2}{3}r \) soit \( r = \frac{3}{2}{R_b} \) Si on exprime \( P_{js} \) en fonction de \( R_b \) on obtient \( {P_{jS}} = r{I^2} = \frac{3}{2}{R_b}{I^2} \) |
|
Quelque soit le couplage : \( {P_{jS}} = \frac{3}{2}{R_b}{I^2} \)
| |
Les pertes fer \( p_{fS} \):
Les pertes fer dépendent de \( U \) et \( f \).
Puissance transmise au rotor. \( P_{tr} \) Moment du couple électromagnétique.
\( {P_{tr}} = {P_a} - {P_{jS}} - {P_{fS}} \)
La puissance est transmise au rotor par l'action du champ magnétique tournant dans l'entrefer à la fréquence \( \Omega_S \)
Il lui correspond un couple électromagnétique \( T_{em} \) tel que:
| \( {P_{tr}} = {T_{em}} \cdot {\Omega _S} \) |
La puissance électromagnétique transmise peut être mise en parallèle de la puissance consommée par \( R/g \) : \( {P_{tr}} = 3 \times \frac{R}{g} I'^2 \)
Puissance mécanique au rotor : \( P_{M} \)
Le couple électromagnétique est responsable de la rotation du rotor à la fréquence n.
\( {P_m} = {T_{em}} \cdot \Omega = {T_{em}} \cdot 2\pi \cdot n = {T_{em}} \cdot 2\pi \cdot {n_s}\left( {1 - g} \right) = {P_{tr}}\left( {1 - g} \right) \)
donc
| \( {P_m} = {P_{tr}}\left( {1 - g} \right) \) |
\(\Omega_S > \Omega \) et \( P_{Tr} > P_M \)
La différence entre les deux correspond aux pertes rotoriques.
Pertes joules dans le rotor \( p_{jR} \) .
Si on néglige les pertes magnétiques dans le rotor (faibles fréquences),
\( \begin{array}{l} {P_{Jr}} = {P_{tr}} - {P_{Mec}} = {T_{em}} \cdot {\Omega _S} - {T_{em}} \cdot \Omega \\ \Rightarrow {P_{Jr}} = {T_{em}}\left( {{\Omega _S} - \Omega } \right)\mathop = \limits_{g = \frac{{{\Omega _S} - \Omega }}{{{\Omega _S}}}} \underbrace {{T_{em}} \cdot {\Omega _S}}_{{P_{tr}}} \cdot g \\ \Rightarrow {{P_{Jr}} = g{P_{tr}}}\\ \end{array} \)
| \( {P_{Jr}} = g{P_{tr}} \) |
Détermination des pertes constantes :
Elles correspondent aux pertes fer du stator et les pertes mécaniques:
| \( {p_{coll}} = {p_{fS}} + {p_{meca}} \) |
Elles sont déterminées par un essai à vide. En effet : \( {P_{abs\,vide}} = {p_{fS}} + {p_{meca}} + {p_{jS\,vide}} \)
\( {p_{coll}} = {p_{fS}} + {p_{meca}} = {P_{abs\,vide}} - {p_{jS\,vide}} = \sqrt 3 \cdot U \cdot {I_{vide}} \cdot \cos {\varphi _{vide}} - \frac{3}{2}{R_b}I_{vide}^2 \)
Puissance utile \( P_{u} \) .
Du fait des pertes mécaniques (frottements mécaniques, ventilation du moteur), la puissance utilisable est :
\( {P_u} = {T_u} \cdot \Omega = {P_m} - {p_{méca}}\) et \( {T_u} = \frac{{{P_u}}}{\Omega } \)
| \( {P_u} = {T_u} \cdot \Omega\) |
Rendement
Le rendement est défini par
| \( \eta = \frac{{{P_u}}}{{{P_a}}} = \frac{{{P_u}}}{{{P_u} + pertes}} = \frac{{{P_a} - pertes}}{{{P_a}}} = \frac{{{T_u}2\pi .n}}{{\sqrt 3 UI\cos \phi }} \) |
\( \sum {pertes = {P_{fS{\rm{ }}}} + {\rm{ }}{P_{JS}}{\rm{ }} + {\rm{ }}{P_{JR}}{\rm{ }} + {P_{méca}}} \)
- Remarque
- Si on néglige les pertes autres que rotoriques : \( \eta = {\eta _{rotor}} = \frac{{{P_M}}}{{{P_{tr}}}} = \frac{{(1 - g){P_{tr}}}}{{{P_{tr}}}} = 1 - g \)
| \( \eta < 1-g \) |
Bilan de puissance du MAS A. Chouah
Bilan de puissance en génératrice








