Modèle du transformateur

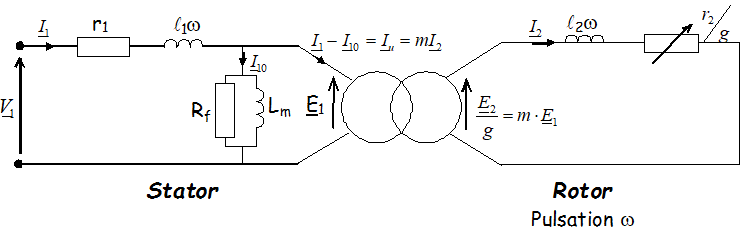
Comme l’analogie est faite avec un transformateur le modèle équivalent est donc le suivant :

$\left\{ \begin{array}{l} {{\underline{V}}_1} - {r_1}{{\underline{I}}_1} - j{\ell _1}\omega {{\underline{I}}_1} = {{\underline{E}}_1} \\ {{\underline{E}}_2} - {r_2}{{\underline{I}}_2} - j{\ell _2}{\omega _R}{{\underline{I}}_2} = 0\,\, \\ \end{array} \right.$

donc

$\left\{ \begin{array}{l} {{\underline{V}}_1} - {r_1}{{\underline{I}}_1} - j{\ell _1}\omega {{\underline{I}}_1} = {{\underline{E}}_1} \\ {{\underline{E}}_2} - {r_2}{{\underline{I}}_2} - j{\ell _2}g\omega {{\underline{I}}_2} = 0\,\, \\ \end{array} \right.$

On divise par g coté rotor

$\frac{{{\underline{E}_2}}}{g} - \frac{{{r_2}}}{g}{\underline{I}_2} - j{\ell _2}\omega {\underline{I}_2} = 0$

Modèle simplifié pertes négligées :

Souvent, on néglige les pertes par rapport à $r1$ et $\ell _1 \omega$.

On peut donc ramener les pertes à la tension $V_1$

Le modèle équivalent simplifié est alors le suivant :

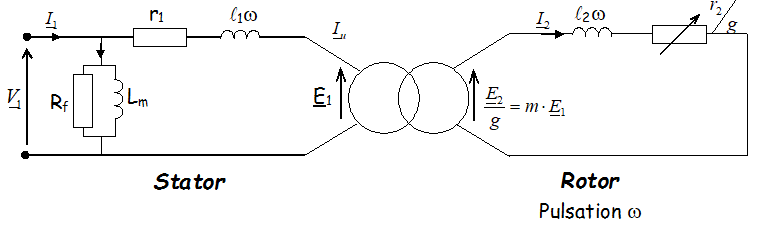
Modèle simplifié ramené au stator :

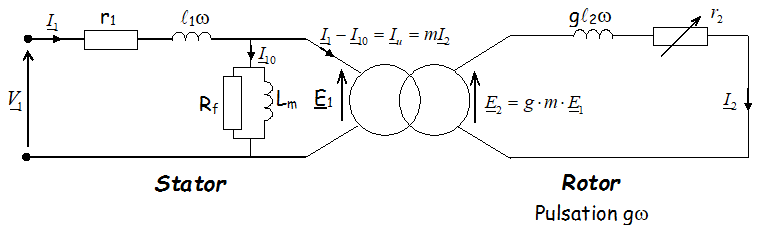
Comme ${\underline{E}_2} = \left( {{r_2} + j{\ell _2}g\omega } \right){\underline{I}_2}$ et en remplaçant $E_2$ et $I_2$.

$\Rightarrow mg{\underline{E}_1} = \left( {{r_2} + j{\ell _2}g\omega } \right)\frac{{{{\underline{I}}_u}}}{m}$

puis en divisant par mg

$\Rightarrow \underline{E}_1 = \left( {{r_2} + j{\ell _2}g\omega } \right)\frac{{{{\underline{I}}_u}}}{m \times mg}$

$\Rightarrow {\underline{E}_1} = \left( {\frac{{{r_2}}}{{g{m^2}}} + j\frac{{{\ell _2}}}{{{m^2}}}\omega } \right){\underline{I}_u}$

ce qui fait apparaitre les résistances et inductances équivalentes ramenées au stator

$\Rightarrow R = \frac{{{r_2}}}{{{m^2}}}$ et ${\ell '_2} = \frac{{{\ell _2}}}{{{m^2}}}$

Soit en ramenant l’impédance secondaire au stator, cela donne le schéma suivant :

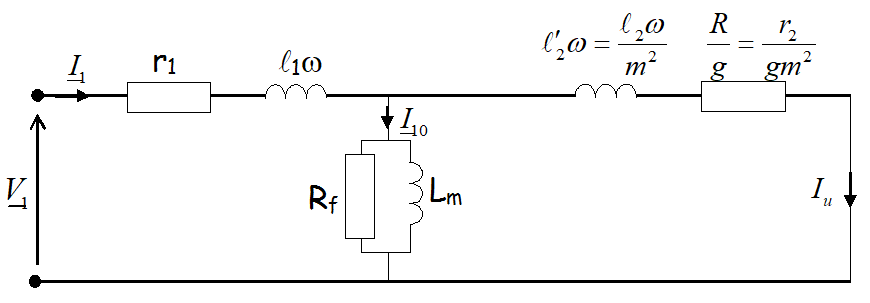
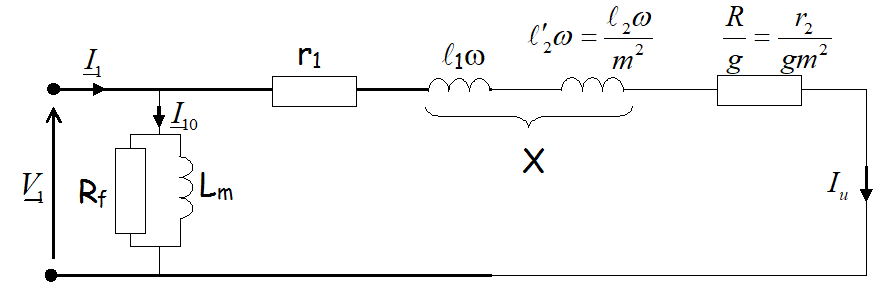
Modèle équivalent d'un enroulement du MAS ramené au stator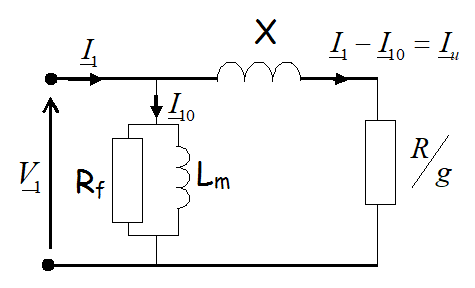

$X$ modélise les inductances de fuite ramenées au stator $R/g$ modélise la puissance électromagnétique transmise $R_f$ modélise les pertes fer $L_m$ inductance magnétisante

La pulsation est $\omega$ pour tout le schéma.

Remarque

les tensions et courants considérés sont ceux d’un enroulement.

Couplage étoile

tension simple et courant de ligne.

Couplage triangle

tension composée et courant dans un enroulement.

---