Wiki du BTS Electrotechnique - SA

Contents [hide]

Nécessité du glissement
Définition du glissement
Valeurs du glissement
Fréquence des courants rotoriques

Nécessité du glissement

Le stator crée un champ magnétique tournant à la vitesse $\Omega_S=\frac{\omega}{p}$ avec $\omega$ = pulsation des courants statoriques en rad/s. (Ceci provient de la relation connue $n_s = \frac{f}{p}$ avec $n_s$ en tr/s)

Les fem induites au rotor provoquent la circulation de courants induits qui s’opposent à la cause qui leur donne naissance c’est à dire la rotation du champ tournant.

Le rotor tourne à une vitesse $\Omega$ inférieure à la vitesse de synchronisme. (fréquence $n$ proche de $n_s$ : $n < n_S$ )

Il y a donc mouvement relatif du rotor par rapport au champ magnétique tournant statorique, à la fréquence de glissement notée $n_g: n_g = n_S - n$

Définition du glissement

On appelle glissement g d'un MAS le rapport $g = \frac{n_g}{n_S}$

D'où

$g = \frac{{{n_S} - n}}{{{n_S}}} = \frac{{{\Omega _S} - \Omega }}{{{\Omega _S}}}$

$\Omega_S$ en rad/s (pulsation mécanique du champ tournant)
$\Omega$ en rad/s (pulsation mécanique du rotor)
$n$ les mêmes en tr/s ou tr/min
g n'a pas d'unités , il s'exprime en %

Relation déduite de la précédente:

$n = (1-g) n_S$

La pulsation mécanique $\Omega_S$ et la pulsation électrique $\omega$ sont liés par la relation issues des relations du champ tournant:

$f = p \times n_S$ :

avec

f en Hz: fréquence de la tension d'alimentation
$n_s$ en tr/s : vitesse du champ tournant
p : nombre de paire de pôles

en multipliant de chaque côté par $2\pi$

$\omega = p \times \Omega_S$

avec

$\omega$ en rad/s: pulsation de la tension d'alimentation rad/s
$\Omega_s$ en tr/s : vitesse du champ tournant en rad/s
p : nombre de paire de pôles

Valeurs du glissement

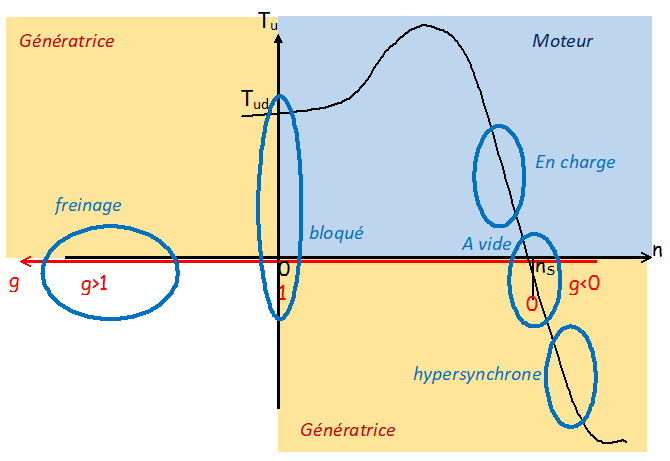
Au démarrage ou rotor bloqué: $n = 0$ donc $g = 1$
A vide : $n \approx ns$ donc $g = 0$
Au freinage par inversion du sens de marche (inversion de l'ordre des phases): $n \approx -n$ donc $g > 1$
En génératrice, le rotor est entrainé au-delà du synchronisme donc $n > ns$ donc $g < 0$
Au régime nominal:

Puissance du MAS	<1kW	>1kW	> 150 kW
g nominal	10 à 20%	3 à 8%	1 à 3%

Fréquence des courants rotoriques

Le rotor, à p paires de pôles, voit le champ statorique tourner par rapport à lui à la fréquence $n_g =g n_S$ . Ces enroulements voient donc apparaître à leurs bornes des fem de fréquences

La fréquence et la pulsation des courants rotoriques sont données par:

$f_r = p n_g = p g n_s = g f$

$\omega_r = \omega_g = p \Omega_g = p (\Omega_s - \Omega) = p g \Omega_s = g \omega$

Exemple : f = 50 Hz ; g = 3% alors la fréquence des courants rotoriques est de $f_R = 1,5 Hz$

Conséquence : le rotor produit un champ magnétique tournant appelé champ magnétique de réaction d'induit

Sa fréquence de rotation par rapport au rotor est $\frac{f_R}{p}=\frac{gf}{p}=gn_S=n_g$ avec $\Omega g=\frac{\omega_R}{p}$ .

La fréquence de rotation du champ rotorique par rapport au stator $= n_g+n = gn_S+n =n_S$ . (vitesse du champ tournant rotorique par rapport au stator $=\Omega+\Omega_g=\Omega_S$ ) .

Ce champ se superpose à celui dû au stator et se déplace à même fréquence $n_s$ . On a bien deux champs tournants synchrones.

Glissement

Nécessité du glissement

Définition du glissement

Valeurs du glissement

Fréquence des courants rotoriques