Descriptions des courbes du triphasé

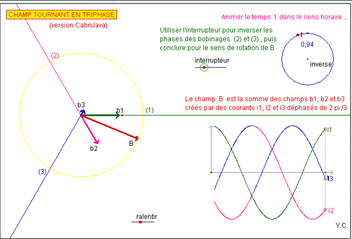
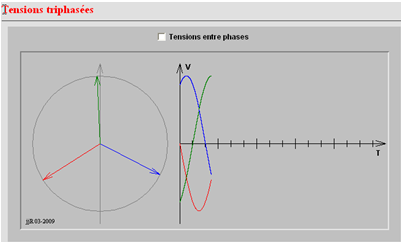
Représentation temporelle

Les trois tensions entre phase et neutre sont dites simples et vérifient \( \left\{ \begin{gathered} {v_1}(t) = \underbrace {V\sqrt 2 }_{\hat V}\sin \omega t \hfill \\ {v_2}(t) = V\sqrt 2 \sin \left( {\omega t - \frac{{2\pi }}{3}} \right) \hfill \\ {v_3}(t) = V\sqrt 2 \sin \left( {\omega t - \frac{{4\pi }}{3}} \right) \hfill \\ \end{gathered} \right. \)

Ismail Sadky Chapitre 3.1 Triphasé - Tension simple représentation de Fresnel (0'09")

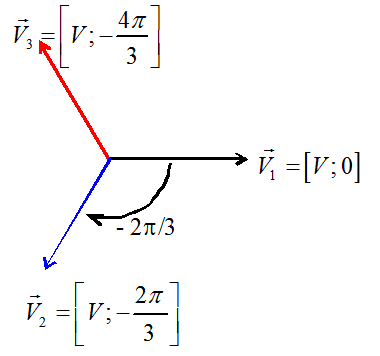
Représentation de Fresnel

\( {\vec V_1} + {\vec V_2} + {\vec V_3} = \vec 0 \)

Nombres complexe associés

Préambule mathématique

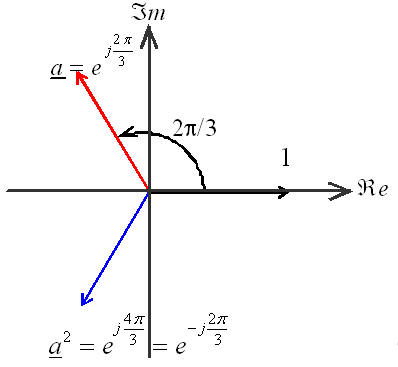
Soit le nombre complexe

\( \underline{a} = {e^{j\frac{{2\pi }}{3}}} = {e^{ - j\frac{{4\pi }}{3}}} = - \frac{1}{2} + j\frac{{\sqrt 3 }}{2} \)

alors

\( \underline{a}^2 = {e^{j\frac{{4\pi }}{3}}} = {e^{ - j\frac{{2\pi }}{3}}} = - \frac{1}{2} - j\frac{{\sqrt 3 }}{2} \)

et l’on peut remarquer que \( 1 + \underline{a} + \underline{a}^2 = 0 \)

Notation des tensions simples

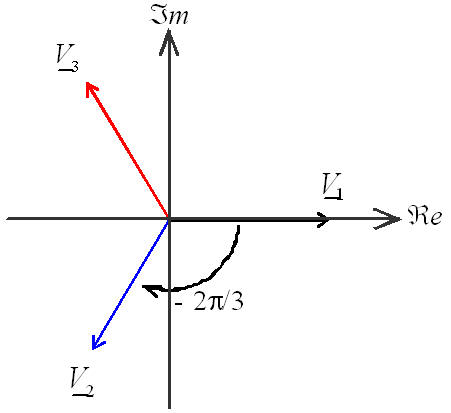
\( \left\{ \begin{gathered} {v_1}(t) = \hat V{e^{j\varpi t}} & \hfill \\ {v_2}(t) = \hat V{e^{j\left( {\omega t - 2\pi /3} \right)}} \hfill \\ {v_3}(t) = \hat V{e^{j\left( {\omega t - 4\pi /3} \right)}} \hfill \\ \end{gathered} \right. \)

\( \left\{ \begin{gathered} {v_1}(t) = \left[ {V;0} \right] \hfill \\ {v_2}(t) = \left[ {V; - 2\pi /3} \right] \hfill \\ {v_3}(t) = \left[ {V; - 4\pi /3} \right] \hfill \\ \end{gathered} \right. \)

\( \left\{ \begin{gathered} {v_1}(t) = \underline{V}_1 \hfill \\ {v_2}(t) = \underline{V}_2 = \underline{a}^2 \underline{V}_1 \hfill \\ {v_3}(t) = \underline{V}_3 = \underline{a} \underline{V}_1 \hfill \\ \end{gathered} \right. \)

et comme \( \underline{V}_1 + \underline{V}_2 + \underline{V}_3 = \underline{V}_1 + \underline{a}^2 \underline{V}_1 + \underline{a} \underline{V}_1 \)

donc \( \underline{V}_1 + \underline{V}_2 + \underline{V}_3 = \underline{V}_1 \left( 1 + \underline{a} + \underline{a}^2 \right) \)

et comme \( 1 + \underline{a} + \underline{a}^2 = 0 \)

alors \( \underline{V}_1 + \underline{V}_2 + \underline{V}_3 = 0 \)

Animations