Les différents couplages s'appliquent aux sources ou aux charges
Couplage étoile des sources
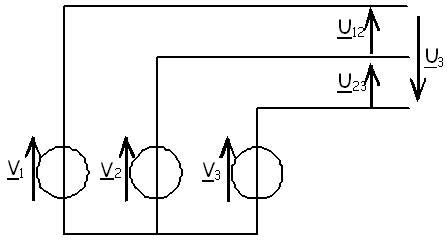
Les trois sources qui nécessiteraient 6 fils sont couplées de façon à n’avoir que 3 fils .
Le neutre
Le point commun aux trois tensions est appelé le neutre.
Les tensions simples
Les trois tensions ainsi créées sont appelées tensions simples ou tension Phase-Neutre et sont souvent notés \( V \) en majuscule.
L'indice indique la tension considérée prise par rapport au neutre. \( \left\{ \begin{gathered} v_{1}= v_{1N} = {v_1} - {v_N} \hfill \\ v_{2}= v_{2N} = {v_2} - {v_N} \hfill \\ v_{3}= v_{3N}= {v_3} - {v_N} \hfill \\ \end{gathered} \right. \)
Les tensions composées
Les tensions composées sont les différences de potentiels entre phases : \( u_{ij} = v_{i} - v_{j} \) et sont souvent notées \( U \).
Ces trois tensions forment également un système équilibré direct.
Leur amplitude est liée au tension simple etl que
| \( U = V\sqrt 3 \) |
Ex: Si la tension simple vaut V = 220 volts, alors U = 380 volts)
Les tensions composées sont liées aux tensions simples par les relations:
\( \left\{ \begin{gathered} {u_{12}} = {v_1} - {v_2} \hfill \\ {u_{23}} = {v_2} - {v_3} \hfill \\ {u_{31}} = {v_3} - {v_1} \hfill \\ \end{gathered} \right. \)
donc
|
\( \left\{ \begin{gathered} {u_{12}}(t) = \underbrace {U\sqrt 2 }_{\hat U}\sin \left( {\omega t + \frac{\pi }{6}} \right) \hfill \\ {u_{23}}(t) = U\sqrt 2 \sin \left( {\omega t - \frac{\pi }{2}} \right) \hfill \\ {u_{31}}(t) = U\sqrt 2 \sin \left( {\omega t - \frac{{7\pi }}{6}} \right) \hfill \\ \end{gathered} \right. \) |
\( \left\{ \begin{gathered} \vec U_{12} = \vec V_1 - \vec V_2 \hfill \\ \vec U_{23} = \vec V_2 - \vec V_3 \hfill \\ \vec U_{31} = \vec V_3 - \vec V_1 \hfill \\ \end{gathered} \right. \) |
| et à chaque instant \( {u_{12}} + {u_{23}} + {u_{31}} = 0 \) | et à chaque instant \( \vec U_{12} + \vec U_{23} + \vec U_{31} = 0 \) |
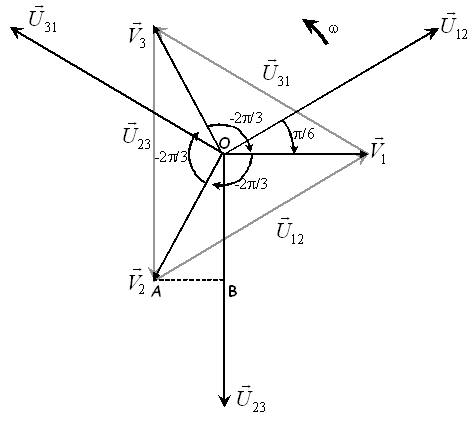
et les vecteurs de Fresnel associés donnent \( {{\vec U}_{12}} + {{\vec U}_{23}} + {{\vec U}_{31}} = \vec 0 \)
On retiendra le résultat important reliant une tension simple à la tension composée :
| \( U = V\sqrt 3 \) |
- Méthode approchée : la mesure des deux vecteurs nous permet de vérifier ce rapport
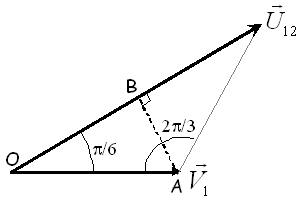
- Méthode géométrique : dans le triangle formé par V et U, deux angles sont de 30° et un de 120° .
\( U = 2 \times OB \) et \( cos \pi/6 = OB/OA \)
\( \Rightarrow U = 2 \times OA \times cos(\pi/6) \)
\( \Rightarrow U = 2 \times V \times cos(\pi/6) = V \sqrt{3} \)
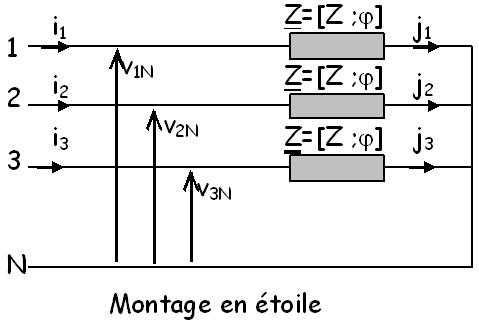
Couplage étoile des charges
Charges équilibrées
Lorsque la distribution triphasée alimente une étoile symétrique où chaque branche présente la même impédance \( \underline{Z} = \left[ {Z;\varphi } \right] \)
|
\( \left\{ \begin{gathered} \underline{I}_1 = \frac{\underline{V}_{1N}}{\underline{Z}} = \left[ {\frac{V}{Z}; - \varphi } \right] = \frac{V}{Z}{e^{j\left( {\omega t - \varphi } \right)}} \hfill \\\underline{I}_2 = \frac{\underline{V}_{2N}}{\underline{Z}} = \left[ {\frac{V}{Z}; - \varphi - \frac{2\pi}{3}} \right] = \frac{V}{Z}{e^{j\left( {\omega t - \varphi - \frac{2\pi}{3}} \right)}} \hfill \\\underline{I}_3 = \frac{\underline{V}_{3N}}{\underline{Z}} = \left[ {\frac{V}{Z}; - \varphi - \frac{4\pi}{3}} \right] = \frac{V}{Z}{e^{j\left( {\omega t - \varphi - \frac{4\pi}{3}} \right)}} \hfill \\ \end{gathered} \right.\) |
 |
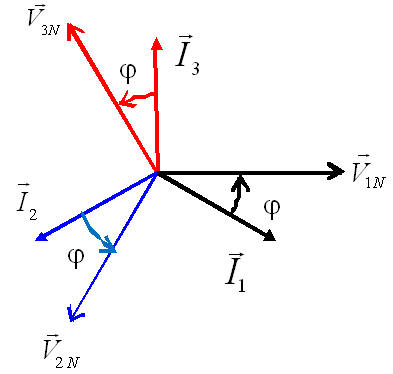 |
On a a chaque instant: \( i_1 + i_2 + i_3 = 0 \) soit en complexe \( \underline{I}_1 + \underline{I}_2 + \underline{I}_3 = 0 \). Le neutre n’est donc pas nécessaire sauf en cas de dissymétrie accidentelle, son absence pourrait nuire au bon fonctionnement des branches de l'étoile
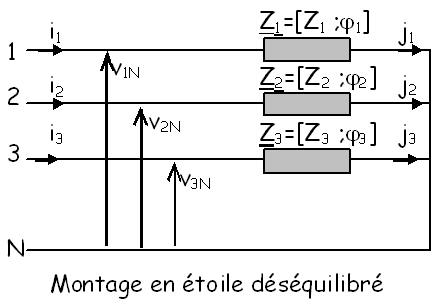
Charges déséquilibrées avec neutre
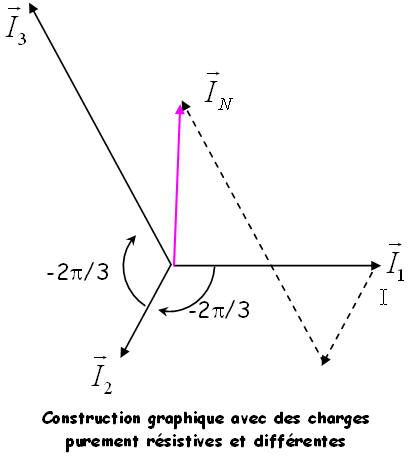
Les récepteurs de nature de puissances différentes sont reliés d'une part à un fil de phase, d'autre part au fil neutre. Le courant dans le fil neutre est la somme vectorielle des courants dans les trois fils de phase.
\( \overrightarrow {{I_1}} + \overrightarrow {{I_2}} + \overrightarrow {{I_3}} = \overrightarrow {{I_N}} \)
Remarque : Le fil neutre est nécessaire sinon les récepteurs seraient soumis à des tensions différentes et risqueraient d'être détruits. Une surtension peut apparaître aux bornes d'un récepteur.
|
\( \left\{ \begin{gathered} \underline{I}_1 = \frac{\underline{V}_{1N}}{\underline{Z}_1} = \left[ {\frac{V}{Z_1}; - \varphi_1 } \right] = \frac{V}{Z_1}{e^{j\left( {\omega t - \varphi_1 } \right)}} \hfill \\\underline{I}_2 = \frac{\underline{V}_{2N}}{\underline{Z_2}} = \left[ {\frac{V}{Z_2}; - \varphi_2 - \frac{2\pi}{3}} \right] = \frac{V}{Z_2}{e^{j\left( {\omega t - \varphi_2 - \frac{2\pi}{3}} \right)}} \hfill \\\underline{I}_3 = \frac{\underline{V}_{3N}}{\underline{Z_3}} = \left[ {\frac{V}{Z_3}; - \varphi_3 - \frac{4\pi}{3}} \right] = \frac{V}{Z_3}{e^{j\left( {\omega t - \varphi_3 - \frac{4\pi}{3}} \right)}} \hfill \\ \end{gathered} \right.\) |
 |
 |
Charges déséquilibrées sans neutre
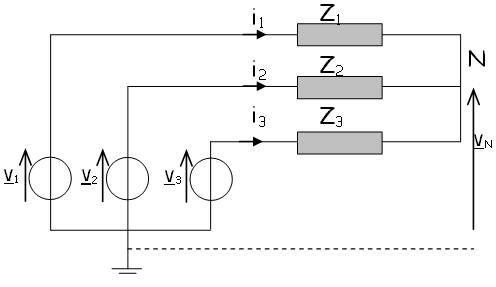
Le potentiel de neutre de la charge est donc libre et se déplace par rapport à celui du réseau.
Le système des courants et des tensions est dissymétrique.
L'abandon du neutre présente le risque de générer de fortes surtensions sur certaines phases
D’après le théorème de Millman qui écrit la loi des nœuds des courants énoncés ci-dessous:
\( \left\{ \begin{gathered} \underline{I}_1 = \frac{\underline{V}_1-\underline{V}_N}{\underline{Z}_1} \hfill \\ \underline{I}_2 = \frac{\underline{V}_2-\underline{V}_N}{\underline{Z}_2} \hfill \\ \underline{I}_3 = \frac{\underline{V}_3-\underline{V}_N}{\underline{Z}_3} \hfill \\ \hfill \\ \end{gathered} \right. \)
L'application du théorème donne
\( \underline{V}_N = \frac{\underline{Y}_1 \cdot \underline{V}_1 + \underline{Y}_2 \cdot \underline{V}_2 + \underline{Y}_3 \cdot \underline{V}_3 }{\underline{Y}_1 + \underline{Y}_2 + \underline{Y}_3} \)
avec \( \underline{Y} = \frac{1}{Z} \)





