Alors que le courant monophasé nécessite deux fils : la phase (potentiel v) et le neutre (potentiel nul), le courant triphasé comporte quatre fils : trois phases (potentiels \( V_1 \), \( V_2 \) et \( V_3 \)) et un seul neutre (Pot- 0)
Les lignes triphasées servent à la distribution des fortes quantités de puissances électriques.
Avantages:
- Le triphasé permet de diminuer par 3 le courant des lignes de transport pour une même puissance P.
- Le triphasé permet de transporter le double de puissance qu'en monophasé à section de câble identique.
- Le triphasé permet de transporter une puissance P avec deux fois moins de cuivre que le monophasé.
- Le triphasé permet de transporter des tensions facilement utilisables pour des forces motrices.
- Les pertes en lignes du triphasé sont 2 fois plus petites qu'en monophasé pour une puissance véhiculée identique et une densité de courant identiques.
- Le triphasé permet aussi d'annuler la puissance fluctuante
Volume de cuivre pour transporter une puissance P en monophasé et triphasé
| Schéma | Si on véhicule la même puissance P en monophasé et triphasé | On fixe la densité de courant j(A/m²) égale dans tous les cas | On peut en déduire une section | Et donc un volume de cuivre |
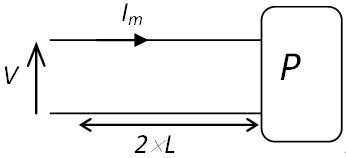
| \( P = V{I_m} \) | \( {I_m} = \frac{P}{V} = j \times {S_m} \) | \( {S_m} = \frac{P}{{V \times j}} \) | \( {V_{o{l_m}}} = 2 \times L \times {S_m} \) \( \Rightarrow {V_{o{l_m}}} = 2 \times L \times \frac{P}{{V \times j}} \) |
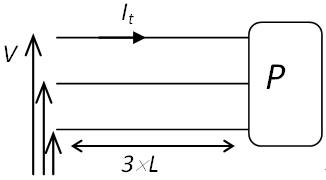
| \( P = 3V{I_t} \) | \( {I_t} = \frac{P}{3V} = j \times {S_t} \) | \( {S_t} = \frac{P}{{3 \times V \times j}} \)
la section nécessaire pour le triphasé est donc 3 fois plus petite que celle du monophasé. | \( {V_{o{l_t}}} = 3 \times L \times {S_t} \) \( \Rightarrow {V_{o{l_t}}} = 3 \times L \times \frac{P}{{3 \times V \times j}} \) |
Le rapport des sections est tel que \( S_m = 3 \times S_t \).
Si on effectue le rapport des volumes de cuivre nécessaires pour transporter la même puissance \( \frac{{{V_{o{l_m}}}}}{{{V_{o{l_t}}}}} = 2 \).
On a donc un volume de cuivre en monophasé double de celui nécessaire en triphasé pour transporter la même puissance.
Pertes Joules pour transporter une puissance P dans des lignes en monophasé et triphasé
Si on s'intéresse aux pertes Joules dans les lignes à densité de courant égales :
| L'expression des pertes Joules | Le courant dans les lignes étant | La résistance de chaque ligne étant | Les pertes Joules peuvent s'exprimer par |
| En monophasé : \( P_{Jm} = 2 \times R_m I_m^2 \) pour le câble de phase et le neutre | \( I_m = \frac{P}{V cos \varphi} \) | \( R_m = \frac{\rho \times \ell}{S_m} \) | \( P_{Jm} = 2 \times R_m I_m^2 \) |
| En triphasé : \( P_{Jt} = 3 \times R_t I_t^2 \) pour les 3 câbles de phases | \( I_t = \frac{P}{\sqrt{3} U cos \varphi} = \frac{P}{3 V cos \varphi} \) | \( R_t = \frac{\rho \times \ell}{S_t} \) | \( P_{Jt} = 3 \times 3 \times R_m (\frac{I_m}{3})^2 = \times R_m I_m^2\) |
| Rapport | \( \frac{I_m}{I_t} = 3 \) | \( \frac{R_t}{R_m} = \frac{S_m}{S_t} = 3 \) | \( \frac{P_{Jm}}{P_{Jt}} = 2 \) |
Pour une densité de courant donné et une puissance véhiculée les pertes Joules seront donc 2 fois plus grandes en monophasé qu'en triphasé .
Remarque : les lignes continues (sous marines par exemple) sont justifiées par les capacités parasites du triphasé qui nécessitent des postes de relèvement du facteur de puissance impossible à implanter sous l’eau. Distance limite du terrestre triphasé : entre 500 et 1000 km





