Reconnaître des éléments en parallèles
Des dipôles sont dits en parallèles ou en dérivation s'ils sont soumis à la même tension
Exemple: Dans le montage suivant
- Les éléments suivants sont en parallèles:
- la résistance
- le condensateur
- l'ensemble de R_bobine en série avec la Bobine
- la diode en série avec la batterie la batterie
- la Source de tension en série avec la R_source

Résistances en parallèle
Résistances en parallèle:

La résistance équivalente à des résistances en parallèle est telle que :
| \( \frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2} \). |
Si l'on a des résistances en parallèles, le courant va se répartir sur les résistances, et la résistance globale est donc plus faible. La conductance équivalente \( G_{eq}=\frac{1}{R_{eq}} \) est la somme des conductances de chaque dipôle.
Dans plusieurs dipôles en parallèle, la loi des nœuds s'applique \( i=i_1+i_2+i_3 \)
- Le courant \( i=\frac{u}{R_{eq}} \)
- Les courants \( i_1=\frac{u}{R_1} \) , \( i_2=\frac{u}{R_2} \) , \( i_3=\frac{u}{R_3} \)
- en regroupant tout dans la loi des nœuds
- en factorisant par u
- puis en simplifiant par u
on retrouve \( \frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} \)
Si l'on n'a que deux résistances alors \( R_{eq}=\frac{R_1 \times R_2}{R_1 + R_2} \)
Mais si l'on en a plus alors la seule généralité que l'on peut écrire est \( \frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} \)
Condensateurs en parallèle
Condensateurs en parallèle:
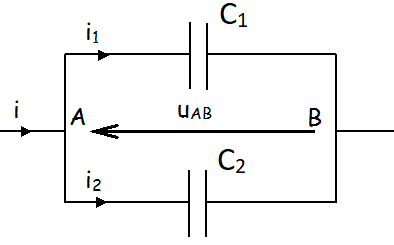
Le condensateur équivalent à des condensateurs en parallèles s'ajoutent :en effet les charges ont plus de surface pour se stocker.
| \( C_{eq}=C_1+C_2 \). |
Bobines en parallèle
Bobines en parallèles :

L'inverse de l'inductance équivalente à des bobines en parallèles est la somme des inverses de chacune des inductances.
\( \frac{1}{L_{eq}}=\frac{1}{L_1}+\frac{1}{L_2} \).
Dipôles quelconques en parallèles

L’impédance équivalente à plusieurs dipôles en parallèles est la somme des admittances complexes:
En effet l'admittance est définie comme l'inverse de l'impédance donc \( \underline{Y} = \frac{1}{\underline{Z}} \)
Quand plusieurs dipôles sont en parallèles leur grandeur commune est la tension.
Dans plusieurs dipôles en parallèles la loi des nœuds s'applique donc: \( \underline{I}_{eq} =\underline{I}_1 + \underline{I}_2 + \underline{I}_3 \)
- \( \underline{I}_1 = \frac{U}{\underline{Z}_1} \)
- \( \underline{I}_2 = \frac{U}{\underline{Z}_2} \)
- \( \underline{I}_2 = \frac{U}{\underline{Z}_2} \)
Modèle parallèle d'une installation
Le modèle parallèle d'une installation monophasée permet de remplacer une installation complexe (de part le nombre et la diversité des charges) par deux dipôles en parallèle qui consommeront les mêmes puissances actives et réactives que l'installation complexe qui consomme \( P_{inst} \) et \( Q_{inst} \).
La résistance du modèle parallèle est telle que \( R_P = \frac{U^2}{P_{inst}}\).
La réactance du modèle parallèle est telle que \( X = \frac{U^2}{Q_{inst}}\)
- \( X_P=L\omega \) si la puissance réactive de l'installation est positive
- \( X_P=\frac{1}{C\omega} \) si la puissance réactive de l'installation est négative





