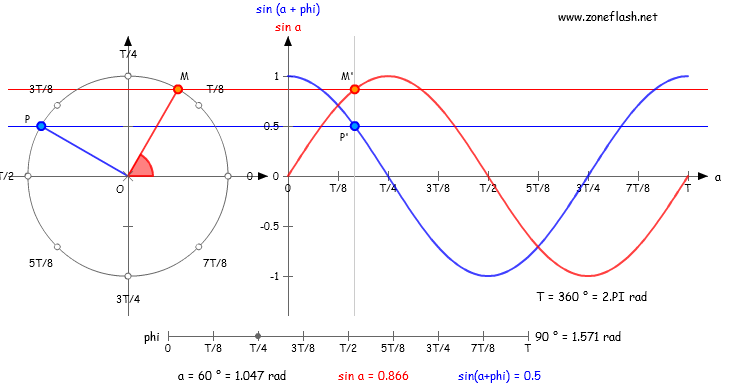
Description qualitative

Une fonction sinusoïdale est une courbe en vague, symétrique par rapport aux abscisses.

On peut la construire en faisant tourner une flèche et projeter sa hauteur à des instants réguliers.

Description mathématique

La fonction sinusoïdale est décrite mathématiquement par les fonctions suivantes:

\(v(t) = V\sqrt 2 \sin (\omega \times t + \phi _u ) \)

avec

  • en minuscule les grandeurs qui dépendent du temps : par exemple \( v \) noté aussi \( v(t) \) est la grandeur tension définie à chaque instant.
  • en majuscule les grandeurs qui ne dépendent pas du temps : par exemple \( V \) la valeur efficace de \( v(t) \)
\( v(t) \) est la valeur instantanée de la tension
\(V_{max} = \hat V = V\sqrt 2 \) est la tension crête ou amplitude, soit la longueur de la flèche qui décrit la sinusoïde.

Chapitre 2.2 Le monophasé - Calculer l'amplitude et la valeur efficace de u (Ismail SADKY) (1'29) https://www.youtube.com/watch?v=bObGme4E9P8?start=6&end=86&rel=0

\( <v(t)>=0 \) la valeur moyenne d'une tension sinusoïdale est nulle
\( V \) est la tension efficace :soit \( V = \frac{V_{max}}{\sqrt 2} \) (relation valable que pour une tension sinusoïdale). La tension efficace est la valeur de la tension continue qui produirait le même effet Joules que cette tension alternative.
\( \omega \) est la pulsation , elle renseigne sur la vitesse de rotation angulaire en \( rad.s^{-1} \)

La vitesse de rotation angulaire dépend du nombre de tours par seconde. Cette information est donnée par la fréquence \( f \) qui indique le nombre d'événements par seconde donc des \( s^{-1} \) ou Hertz (en l’occurrence des tours de la flèche décrivant la sinusoïde). Comme à chaque tour la flèche effectue \( 2 \times \pi \) radians, la pulsation et la fréquence sont donc liés par

\( \omega = 2 \times \pi \times f \)

Chapitre 2.2 Le monophasé - Calculer la pulsation d'une grandeur sinusoïdale (Ismail SADKY) (2'38) https://www.youtube.com/watch?v=yDVGj4QtgDY?start=6&end=153&rel=0

\( T \) est la période. C'est la durée d'un motif qui se répète.
\( f \) est la fréquence. Cela peut être vu comme le nombre tours par seconde effectués par la flèche permettant de décrire la sinusoïde. Elle dépend donc du temps mis par la flèche pour faire un tour que l'on appelle période T en secondes (s). La fréquence compte le nombre de ces rotations en une seconde. Ces deux grandeurs sont donc liées par
\( f = \frac{1}{T} \)
\(\omega \times t + \phi_u\) est la phase instantanée à l'instant. C'est donc l'angle formé par le vecteur à l'instant t
\(\phi _u\) est la phase à l'origine est l'angle à partir duquel commence la sinusoïde. Diverses méthodes permettent de trouver cette phase et son signe

  • par un dessin du vecteur décrivant la sinusoïde à l'instant t=0 puis en mesurant l'angle de ce vecteur.(A voir sur l'applet en dessous)
  • à l'aide du temps mis par la courbe pour passer d'une phase instantanée nulle au temps t=0 ou l'inverse. Ce temps \( \Delta t \) donne l'angle \( \phi_u=\frac{2 \pi \times \Delta t}{T}\) en radians ou \( \phi_u=\frac{360 \times \Delta t}{T}\) en degrés. Le signe dépend de la position du vecteur décrivant cette courbe.
Une relation classique de la phase à l'origine est donc
\( \phi_u = \frac{360 \times \Delta t}{T}\)
avec
  • \( \phi_u \) l'angle en degrés
  • \( \Delta t\) le temps séparant le passage de la courbe par 0 et en montant et l'origine.
  • \( T \) la période de la sinusoïde
la même expression avec l'angle en radians
\( \phi_u = \frac{2 \pi \times \Delta t}{T}\)
  • à l'aide de l'ordonnée à l'origine de la courbe:
En effet l'équation de la courbe est telle que à t=0 :\(v(0) = V\sqrt 2 \sin (\omega \times 0 + \phi_u ) \)
donc \(v(0) = V\sqrt 2 \sin ( \phi_u ) \)
donc \(\phi_u = arcsin \left( \frac{v(0)}{V\sqrt 2} \right) \)

Exemple:

  • la valeur crête est : \( V_{max}=3 car \times 0.5 V/car = 1.5 V \)
  • la valeur efficace est donc : \( V=\frac{V_{max}}{\sqrt{2}}= \frac{1.5}{\sqrt{2}} V \)
  • la période est : \( T= 10 car \times 2.5 ms/car = 10 \times 2.5 = 25 ms = 25 \cdot 10^{-3} s \)
  • la fréquence est donc : \( f= \frac{1}{25 \cdot 10^{-3}}= 40 Hz \)
  • la pulsation est donc : \( \omega = 2 \times \pi \times 40 = 251 rad/s \)
  • la phase à l'origine est donnée par \( \Delta t = 1.3 \times 2.5 = 3.25 ms \) donc \( \varphi = \frac{2 \times \pi \times 3.25}{25} = 0.81 rad \) ou 45.8°. La courbe partant du bas , l'angle est négatif, soit \( \varphi = - 0.81 rad \)
  • donc \(v(t) = 3 \sin (251 t - 0.81) \)

Somme de deux fonctions sinusoïdales

L'addition de deux grandeurs sinusoïdales nécessite de faire la somme à chaque instant des valeurs des deux grandeurs à additionner. Cette opération est lourde et fastidieuse à réaliser sans un tableur?. C'est pourquoi d'autres outils sont utilisés afin de faciliter les opérations sur des grandeurs sinusoïdales:

Auto-évaluation

Auto-évaluation du Lycée Charles Augustin Coulomb:

Vidéos

Cours IUT GEII Cachan 40'28"
https://youtu.be/AIDfd5_M434
Voyage en électricité : Ep 22 (5'55")
  • Explication sur le tracé de la sinusoïde (projection d'une flèche tournante sur la verticale)
  • Explication sur la période, fréquence
  • Courant et tension dans une résistance
  • Tension efficace
https://youtu.be/8rXUzIjPwnc?start=14

Autres ressources