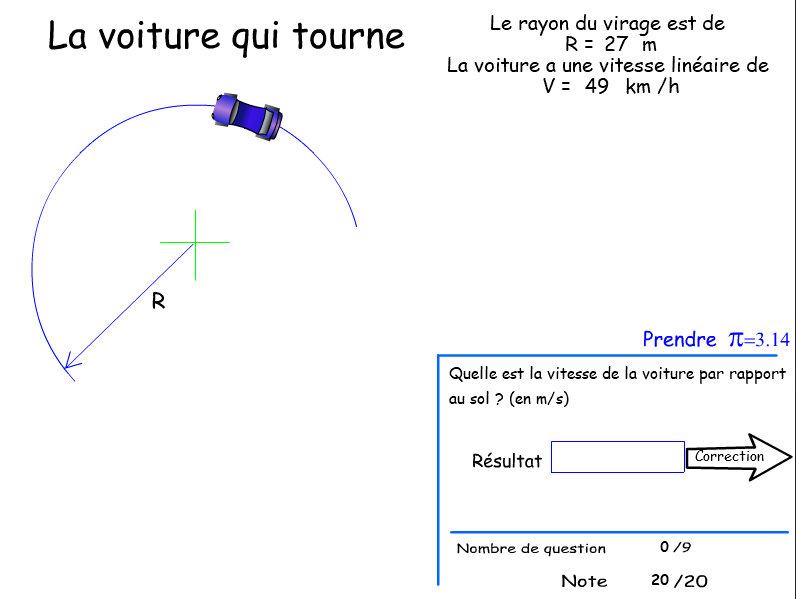
Angle en rad:
L'arc de cercle \( \ell \) parcouru par un rayon \( R \) balayant un angle \( \theta \) est tel que
| \( \theta = \frac{\ell}{R} \) |
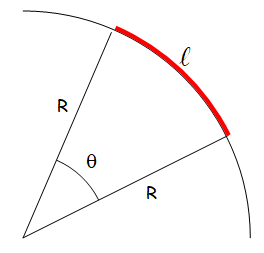
Vitesse angulaire en rad.s-1:
La vitesse angulaire \( \Omega \) en \( rad \cdot s^{-1} \) est une variation d'angle par unité de temps soit:
| \( \Omega = \frac{{d\theta }}{{dt}} \) |
Si l'on s'intéresse à un point situé à une distance \( R \) de l'axe de rotation, alors sa vitesse linéaire \( v \) (en \( m/s \)) est telle que:
| \( v = {R} \times \Omega \) |
Pour passer d'une vitesse de rotation \( n \) en tours par minute ou rpm (round per minutes)
à une vitesse de rotation \( \Omega \) en rad/s, il suffit de se souvenir qu'un tour équivaut à \( 2\pi \) radians
donc \( \Omega =\frac{2\pi \times n}{60} \)
Accélération angulaire en rad.s-2:
| \( \frac{{d\Omega }}{{dt}} = \frac{{{d^2}\theta }}{{d{t^2}}} \) |
Pour s'entrainer:
Source:ECLigne