Exemple de système en rotation
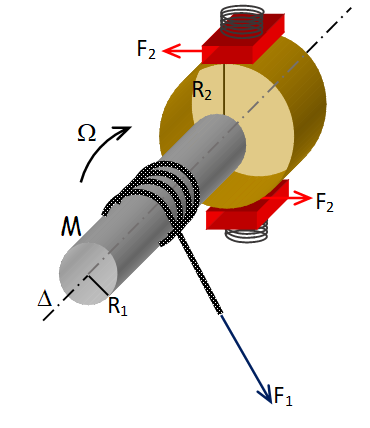
Le dispositif suivant peut être vu comme un frein (deux cales rouges contraintes sur le disque orange de rayon \( R_2 \) générant une force de frottement \( F_2 \)) retenant ainsi la corde déroulant le long du cylindre gris de rayon R1 sur laquelle est appliquée une force de traction \( F_1 \).
Le couple moteur généré par la force \( F_1 \) est donc \( {C_m} = {F_1} \times {R_1} \)
Le couple résistant généré par le frein est donc \( {C_r} =2 {F_2} \times {R_2} \)
- si les couples sont égaux il n’y a pas de rotation, ou la vitesse de rotation reste constante
- si le couple moteur est supérieur au couple résistant la rotation va accélérer dans le sens de la force \( F_1 \)
- si le couple de frottement est supérieur au couple moteur la rotation va décélérer jusqu’à s’arrêter
Plus le moment d'inertie \( J \) de l’ensemble en rotation est élevée, plus il sera long de générer une accélération ou une décélération \( \frac{{d\Omega }}{{dt}} \).
La généralisation de l'exemple précédent est traduit par le principe fondamental de la dynamique des systèmes en rotation.
Principe fondamental de la dynamique des systèmes en rotation
Le principe fondamental de la dynamique traduit le fait qu'une variation de vitesse provient d'un couple résultant non nul.
Les conséquences sont les suivantes:
- Si on suppose un système en rotation préalablement lancé et sans frottement sa vitesse sera constante (pas de couple exercé)
- Si la somme des couples exercés sur un solide en rotation est nulle sa vitesse de rotation est constante
- Si la somme des couples exercés diffère de 0, sa vitesse va varier.
- augmentera si la somme des couples est positive
- diminuera si la somme des couples est négative
\( \sum {C} = J\frac{{d\Omega }}{{dt}} \)
| \( \sum {C_{moteur}} - \sum {C_{résistant}}= J\frac{{d\Omega }}{{dt}} \) |
avec
- C les couples en N.m
- J le moment d'inertie en kg.m2
- \( \frac{{d\Omega }}{{dt}} \) la variation de vitesse angulaire soit l'accélération angulaire en rad.s-2





