Modèle proposé
Si on adopte le modèle suivant pour la bobine:
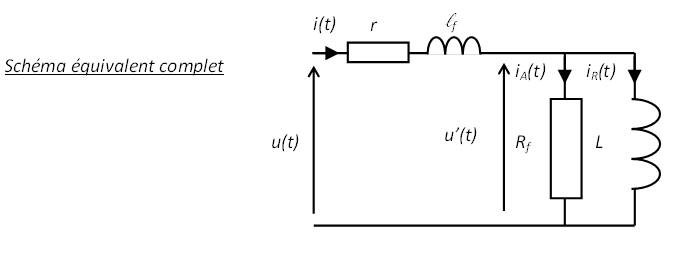
Mesure en continu: détermination de \( r \)
Comme en continu le modèle de la bobine se ramène à sa résistance interne, une mesure de U et I en continu permet de déterminer r.
\( r=\frac{U_{DC}}{I_{DC}} \)
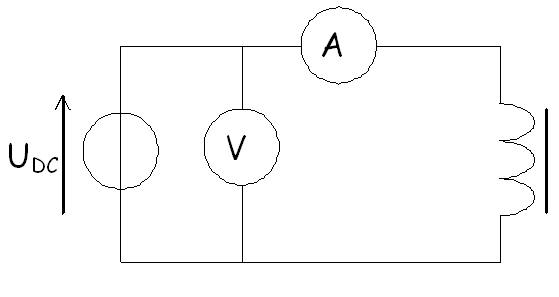
Mesure en alternatif basse fréquence: détermination des paramètres \( R_f \) et \( L \)
En alternatif, une mesure des puissances consommées permettra de déterminer la résistance \( R_f \).
Le montage suivant permet de mesurer, U, I, P, Q.
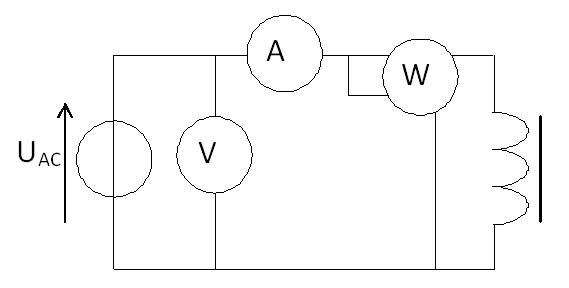
La puissance active absorbée correspond à \( P = r I^2 + \frac{U'^2}{R_{f}}\). Si on considère la chute de tension dans \( \ell_f \) et \( r \) faible alors \( U \approx U'\) donc
\( R_{f} = \frac{U'^2}{P - r I^2} \).
En faisant la même approximation pour la réactance magnétisante, et donc l'inductance : \( X = L\omega = \frac{U'^2}{Q} \)
Mesure en alternatif haute fréquence (>MHz):
Le modèle haute fréquence fait apparaitre un condensateur en parallèle sur l'inductance traduisant ainsi le phénomène de résonance apparaissant à hautes fréquences et la baisse d'impédance qui s'ensuit.





