Détermination de l'inductance
Si on suppose
- un matériau exploité dans sa zone linéaire: pas de saturation ni de phénomène d'hystérésis
- pas de fuite de flux
Dans une bobine, si on considère que la ligne de champ n'existe que dans la bobine (pas de fuite de flux), l’écriture de la loi d’Hopkinson donne:
\( \Re \varphi =Ni \) avec \( \Re = \frac{\ell }{\mu S} \) donc le flux créé par la bobine \( \varphi = S \times B = S \times \mu H = \frac{S \mu N i}{\ell} \)
Ce flux, quand il varie, induit dans chaque spire de la bobine une tension \( u_{1spire}= -e = \frac{d \varphi}{dt} \).
Comme la bobine est constituées de N spires la tension \( u_{Nspire}=u= N \frac{d \varphi}{dt} \)
La tension induite dans une bobine est donc \( u= N \frac{d \varphi}{dt}= N \frac{d(\frac{S \mu N i}{\ell})}{dt} = N^2 \frac{S \mu }{\ell} \frac{di}{dt}\)
Si on remplace \( \frac{\ell }{\mu S} \) par \( \Re \)
Alors \( u(t) = \underbrace {\frac{{{N^2}{\mu}S}}{\ell }}_L\frac{di}{dt} \) devient \( u(t) = \underbrace {\frac{{{N^2}}}{\Re }}_L\frac{{di}}{{dt}} \) ce qui fait apparaitre un coefficient de proportionnalité liant la tension d'une bobine à la variation du courant la traversant:
| \( L = \frac{{{N^2}{\mu}S}}{\ell } = \frac{N^2}{\Re}\) |
- L: inductance de la bobine en Henry (H)
- N: le nombre de spires de la bobine
- \( \mu \): la perméabilité absolue du matériau avec \( \mu=\mu_r \mu _0 \)
- S: la section de la bobine en m²
- \( \ell \): la longueur de la bobine en m
Si la bobine entoure un noyau ferromagnétique, avec de très faibles pertes fer et tant que l'excitation magnétique ne sature pas le matériau alors la relation précédente est vraie
Ce coefficient L reste constant tant que la perméabilité \( \mu \) ne change pas.
La relation précédente est une approximation et omet que les lignes de champs d'une bobine forment des ellipses autour de la bobine. L'écriture de la loi d'Hopkinson est donc modifiée et donne lieu à des expressions
- plus complexes cf wikipédia ou Tavernier si on garde la forme droite de notre solénoïde
- proche de ce que l'on vient d'écrire si l'on considère un solénoïde torique sur de l'air cf ici. En effet dans ce cas les lignes de champ sont bouclées sur l'air et la dimension du parcours des lignes de champ concorde avec la longueur de la bobine
Relation entre flux , inductance et courant
De même cette proportionnalité est retrouvée entre le flux dans une spire et le courant qui la traverse :
En effet comme \( u(t) = L\frac{di}{dt} = N \frac{d\varphi}{dt} \)
On retrouve
| \( \phi = N\varphi = Li \) |
où
- \( \phi \) est le flux vu par l’ensemble des spires
- L l’inductance vue précédemment.
Relation entre champ dans la bobine et tension d'alimentation dans l'hypothèse de Kapp
L'hypothèse de Kapp néglige les fuites et la résistance du fil : \( {\ell _f}\frac{{di(t)}}{{dt}}\,\,{\text{et}}\,r\,i(t)\,\, \ll {\text{à }}\,\,N\frac{{d\phi (t)}}{{dt}} \)
La tension alimentant la bobine est de la forme \( u(t) = U\sqrt 2 \cos \omega t = N\frac{{d\varphi (t)}}{{dt}} \)
donc par intégration on trouve \( \varphi (t) = \frac{{U\sqrt 2 }}{{N\omega }}\sin \omega t \)
Comme \( \varphi = S \times B \) on en déduit \( B(t) = \frac{{\varphi (t)}}{S} = \frac{{U\sqrt 2 }}{{SN\omega }}\sin \omega t = {B_{\max }}\sin \omega t \)
ainsi en identifiant les amplitudes : \( B_{\max } = \frac{{U\sqrt 2 }}{{SN\omega }} \)
on obtient la relation de Boucherot liant la valeur efficace de la tension et le champ maximal:
| \( U = \frac{{2\pi }}{{\sqrt 2 }}{B_{\max }}NSf = 4,44 \times {B_{\max }}NSf \) |
où le flux et la tension sont sinusoïdaux.
La loi d’Hopkinson nous rappelle que \( Ni = \Re \cdot \varphi \) donc \( i = \frac{{\Re \cdot \varphi }}{N} = \frac{\Re }{{{N^2}}}\frac{{U\sqrt 2 }}{\omega }\sin \omega t = \frac{{U\sqrt 2 }}{{L\omega }}\sin \omega t \) et l’on retrouve la définition de l’inductance en régime sinusoïdal : \( Z= L \omega \)
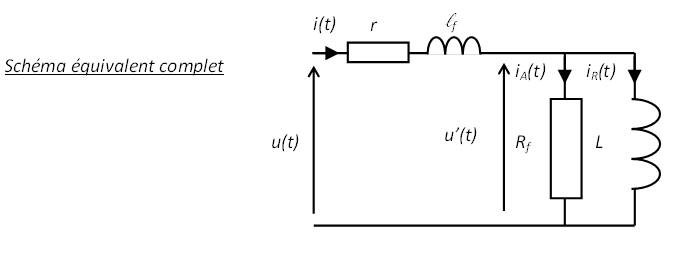
Modèle équivalent de la bobine
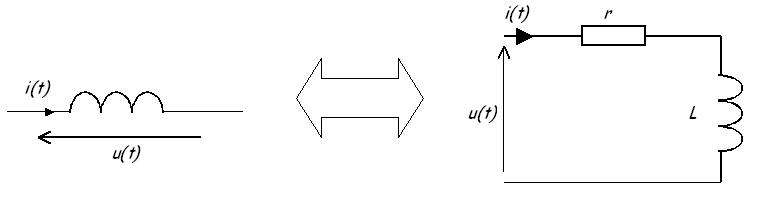
Modèle simple en régime linéaire
Afin de tenir compte de la résistance des fils on ajoute une résistance r en série
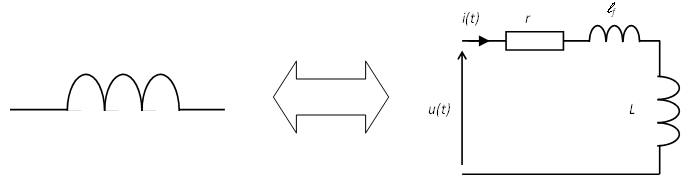
Modèle avec fuites de flux
Démonstration Afin de tenir compte des flux de fuite on ajoute une inductance \( \ell_f \)
Modèle complet en régime non-linéaire
Démonstration Afin de tenir compte des pertes fer on ajoute une résistance en parallèle sur notre inductance \( R_f \)