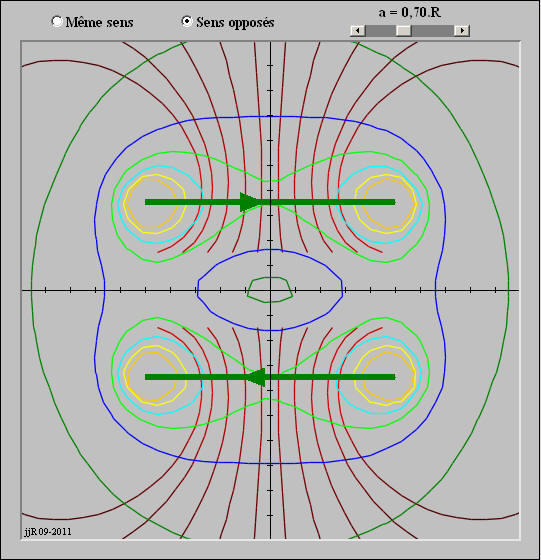
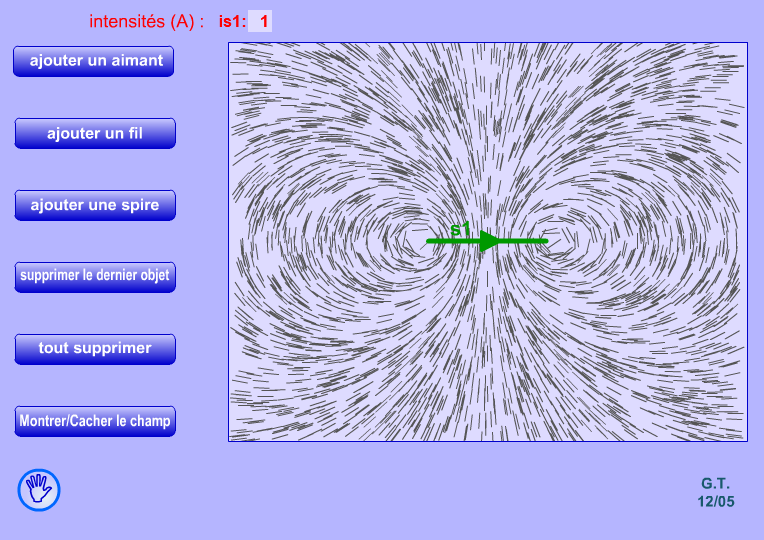
Lignes de champ:
Les lignes de champ sont des lignes imaginaires suivant lesquelles est orienté le champ magnétique.
A l'extérieur d'un aimant ou d'une bobine les lignes de champ vont du Nord vers le Sud.
Lignes de champ magnétique: Département de physique, Cégep de l'Outaouais (1'07")
- 0'00" Attraction répulsion pôles N et S
- 0'08" spectre aimant droit
- 0'22" spectre fil
- 0'35" spectre bobine
- 0'49" force magnétique sur charge en mouvement et force électrique sur toutes les charges
- ..
https://www.youtube.com/watch?v=LZ5wmXbu5vQ
Champ magnétique terrestre

Aimant droit
Le champ magnétique part du pôle Nord vers le pôle Sud

| Animation de Walter Fendt permettant de visualiser les lignes de champ d'un aimant droit. | https://youtu.be/opneAiFcsG4 |
Aimant en U
Le champ magnétique part du pôle Nord vers le pôle Sud

| https://youtu.be/kdomJQvxPZE |
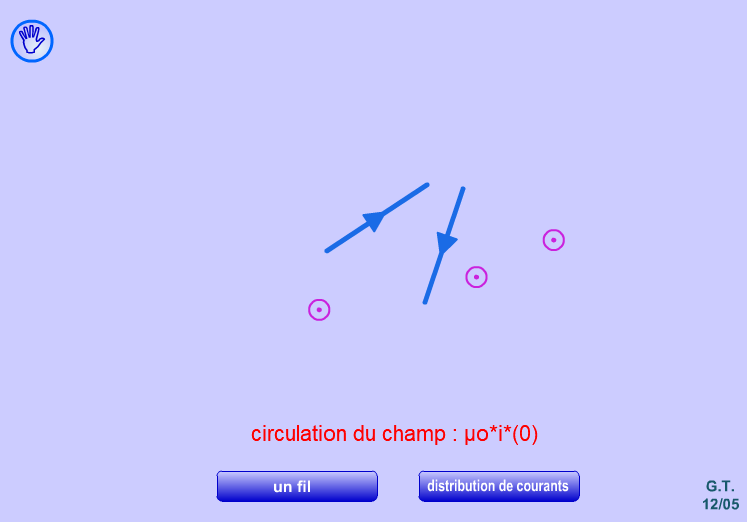
Fil parcouru par un courant
Un fil parcouru par un courant génère un champ magnétique autour de celui-ci dont les caractéristiques sont les suivantes:
- les lignes de champ sont des cercles perpendiculaires au fil et centré sur celui-ci
- l'intensité décroit avec la distance tel que \( \left\| {\vec B} \right\| = \frac{{{\mu _0}I}}{{2\pi r}} \).
- r distance au centre en m
- I intensité du courant en A
- \( \mu_0 \) perméabilité magnétique du vide : \( 4 \pi 10^{-7} \)
- L'orientation du champ suit la règle du
- tire-bouchon : un tire bouchon que l'on visse dans le sens du courant, tournera dans le sens du champ magnétique
ou
- de la main droite (illustrée ci-dessous): la main droite dont le pouce pointe dans le sens du courant a ses doigts qui pointent dans le sens du champ magnétique

| Animation de Walter Fendt | Animation de Geneviève Tulloue de l'université de Nantes, qui permet entre autre de visualiser l'intensité et l'orientation du champ magnétique créé par un fil. | https://youtu.be/z5rLXjhlkjQ |
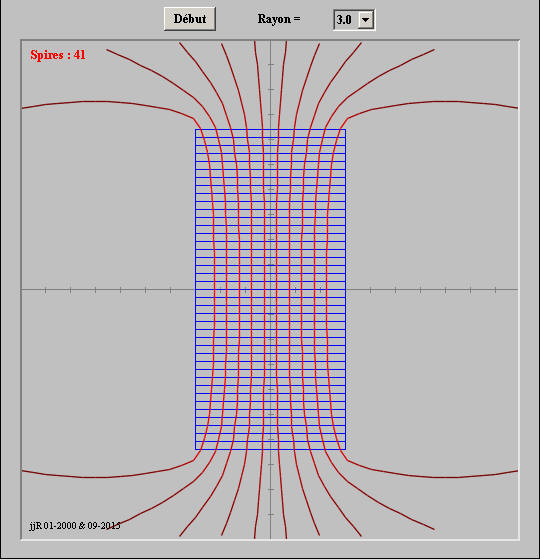
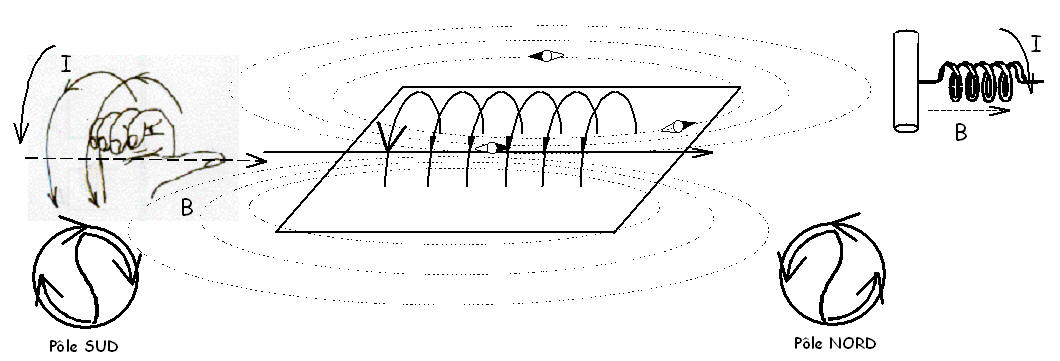
Bobine parcourue par un courant:
Une bobine parcourue par un courant génère un champ magnétique tel que la bobine se comporte comme un aimant.
Si la bobine est dite longue, longueur >> au rayon on parle alors de solénoïde.
- Le champ magnétique part du pôle Nord vers le pôle Sud à l'extérieur de la bobine.
- du Sud vers le Nord à l'intérieur de la bobine et du Nord vers le Sud à l'extérieur de la bobine. Les pôles étant déterminés par la règle de la main droite ou du tire bouchon
- l'intensité du champ magnétique à l'intérieur est tel que \( \left\| {\vec B} \right\| = \frac{{{\mu _0}NI}}{\ell} \).
avec
- \( N \) le nombre de spires
- \( I \) le courante n Ampères
- \( \ell \) la longueur de la bobine en mètres
- \( \mu_0 \) perméabilité magnétique du vide \( \mu_0=4 \pi \cdot 10^{-7} \)
L'orientation du champ suit la règle du
- tire-bouchon (illustrée ci-dessous): un tire bouchon que tourne dans le sens du courant, s'enfoncera dans le sens du champ magnétique
ou
- de la main droite (illustrée ci-dessous): la main droite dont le pouce pointe dans le sens du champ magnétique a ses doigts qui pointent dans le sens du courant
ou
- Si on regarde une face de la bobine (de l'extérieur), le sens du courant dessinera ou une face Nord ou une face Sud
Vecteur champ d’induction magnétique (11'29")
- 0'Générique
- 0'36" le champ magnetique autour d’un solénoide
- 0'55" direction d’un courant dans une boucle
- 9'45" courant induit
|
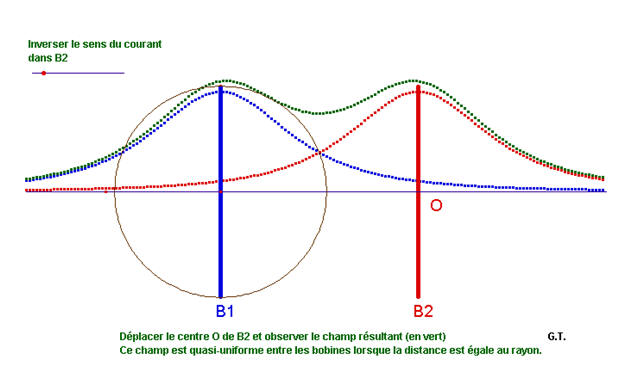
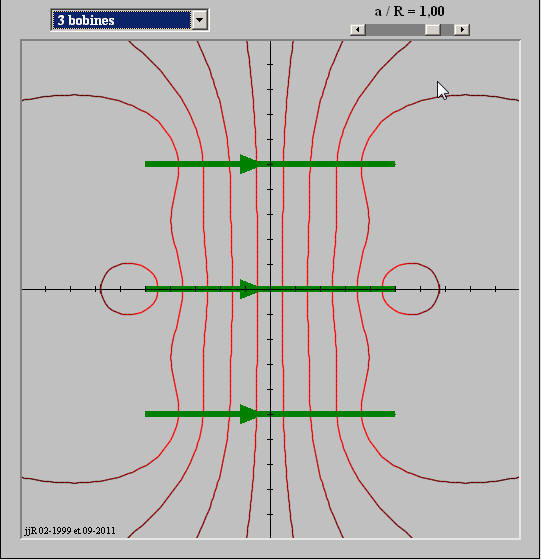
Animation de Geneviève Tulloue de l'université de Nantes, qui permet de visualiser l'intensité de du champ magnétique lors du passage au travers des bobines dites de "Helmholtz". |
Animation de l'université du Mans |
Animation de l'université du Mans |
Bobines d'Helmoltz
Animation de l'université du Mans sur les bobines d'Helmoltz.
Animation sur les lignes de champ
Animation de Geneviève Tulloue de l'université de Nantes, qui permet de visualiser l'orientation du champ magnétique créé par un fil, une bobine, un aimant droit.
Vecteur champ magnétique
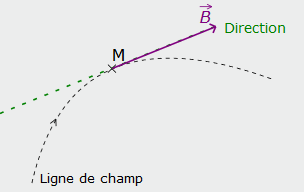
Pour représenter les caractéristiques du champ magnétique en un point de l'espace, on utilise le vecteur champ magnétique généralement noté \( \vec B \) dont les caractéristiques sont les suivantes :
- Point d'application : le point d'observation.
- Direction : tangente à la ligne de champ passant par le point d'observation.
- Sens : Sud Nord de l'aiguille aimantée placée en ce point.
- Longueur: proportionnelle à l'intensité du champ calculé ou mesuré à l'aide d'un teslamètre.
On dit que le champ est uniforme si le vecteur champ magnétique est identique en chaque point de l'espace considéré.
Ordres de grandeur
Le champ magnétique se mesure en Tesla (T).
- 20 µT : champ magnétique terrestre
- quelques 10 mT : aimants ordinaires
- quelques 100 mT :aimants de machines tournantes
- 1 T : champ produit par les enroulements de machines tournantes, transformateurs.
Limites
- 40 T : champ stationnaire produit par plasma, électro aimants supra conducteurs
- 700 T : Champs impulsionnels de laboratoire
Superposition de champ magnétiques:
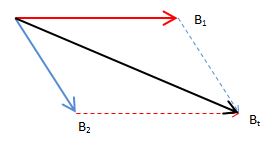
Si plusieurs sources de champ magnétique agissent en même temps, par le principe de superposition, les champs magnétiques de chacune des sources s'additionnent vectoriellement pour donner la résultante finale
\( \vec B_t = \vec B_1 + \vec B_2 \)
Définition
Le champ d’induction magnétique \( \vec B \) traduit l’effet du mouvement des charges électriques :
\( \vec B = \frac{{{\mu _0}}}{{4\pi }}\frac{{q\vec v \wedge {{\vec u}_{PM}}}}{{{r^2}}} \)
avec
- \( \vec B \) champ d’induction magnétique en Tesla (T) orienté de telle manière que \( q\vec v \), \( {\vec u}_{PM} \), \( \vec B \) forment un trièdre direct
- \( \vec v \) vitesse de la charge q en m/s
- q charge électrique en Coulomb
- \( r \) distance de la charge au point d'expression de \( \vec B \) en m
- \( {\vec u}_{PM} \) est le vecteur unitaire porté par PM
- \( \mu_0 \) perméabilité magnétique du vide \( \mu_0=4 \pi \cdot 10^{-7} \)
C’est une grandeur vectorielle dépendant de l’espace (position) et du temps. L’induction s’exprime en tesla (T). Si les charges parcourent un conducteur électrique, on écrit localement la loi de Biot et Savart
\( d\vec B = \frac{{{\mu _0}I}}{{4\pi }}\frac{{d{{\vec \ell }_P} \wedge {{\vec u}_{PM}}}}{{r_{PM}^2}} \)
avec
- \( d{{\vec \ell }_P} \) longueur de circuit portant la charge q
- \( r \) distance de \( d{{\vec \ell }_P} \) au point d'expression de \( d\vec B \) support du vecteur unitaire \( {\vec u}_{PM} \)
La sommation de cette loi permet d’obtenir l’effet de toutes les charges en un point de l’espace. Si le vecteur champ d’induction est identique en tout point de l’espace, le champ est dit uniforme. Dans les problèmes technologiques que nous rencontrerons, l’induction magnétique sera une grandeur connue. Elle ne sera pas à déterminer par les relations précédentes.