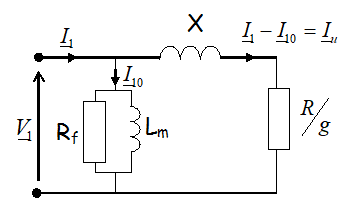
Grâce à l’essai en charge on peut aussi déterminer \( R \) et \( X \) .
Par un bilan des puissances active et réactive (théorème de Boucherot), on détermine les puissances active et réactive dissipées dans R et X mais cette fois on ne peut négliger \( P_{10} \) et \( Q_{10} \) que l’on connait grâce à l’essai à vide.
\({P_{1n}} = {P_{10}} + {P_R} \) et \( {Q_{1n}} = {Q_{10}} + {Q_X} \)
et on en déduit :
\( \left\{ \begin{array}{l} {P_{1n}} = {P_{10}} + 3 \cdot \frac{R}{g} \cdot I_{1n}^2 & \Rightarrow {R = g\frac{{{P_{1n}} - {P_{10}}}}{{3 \cdot I_{1n}^2}}}\\ {Q_{1n}} = {Q_{10}} + 3 \cdot X \cdot I_{1n}^2 & \Rightarrow {X = \frac{{{Q_{1n}} - {Q_{10}}}}{{3 \cdot I_{1n}^2}}}\\ \end{array} \right. \)
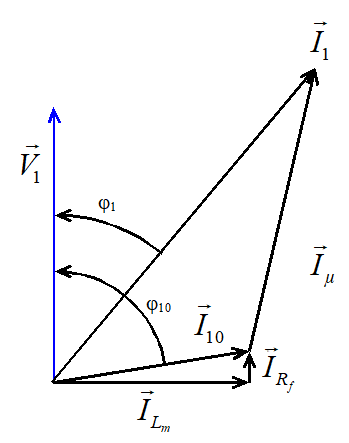
On peut aussi déterminer \( I_µ \) par une construction de Fresnel. \( {\vec I_1} = {\vec I_{10}} + {\vec I_\mu } \Rightarrow {\vec I_\mu } = {\vec I_1} - \vec I{}_{10} \)