Dynamiques des fluides incompressibles
Écoulements permanents ou stationnaires:
Un régime d'écoulement est dit permanent ou stationnaire si les paramètres qui le caractérisent (pression, température, vitesse, masse volumique, ..), ont une valeur constante au cours du temps.
Définitions
- Ligne de courant
- En régime stationnaire, on appelle ligne de courant la courbe suivant laquelle se déplace un élément de fluide.
- Tube de courant
- Ensemble de lignes de courant s'appuyant sur une courbe fermée.
- Filet de courant
- Tube de courant s'appuyant sur un élément de surface dS.
La section de base dS du tube ainsi définie est suffisamment petite pour que la vitesse du fluide soit la même en tous ses points (répartition uniforme).
Équation de conservation de la masse ou équation de continuité
Conservation du débit masse :

En régime stationnaire, le débit massique est le même à travers toutes les sections droites d'un même tube de courant
| \( {Q_m} = \rho \cdot {S_1} \cdot {v_1} = \rho \cdot {S_2} \cdot {v_2} \) |
Remarque : Si un circuit se partage, le débit entrant est égal à la somme des débits sortants
Pendant l'intervalle de temps dt, infiniment petit, la masse dm1 de fluide ayant traversé la section dS1 est la même que la masse dm2 ayant traversé la section dS2.
Les volumes correspondants sont égaux à \( {M_1}M_1^{'}{S_1} \) et \( {M_2}M_2^{'}d{S_2} \) . La conservation de la masse s'écrit \( {\rho _1}{M_1}M_1^{'}d{S_1} = {\rho _2}{M_2}M_2^{'}d{S_2}\ \): soit encore : \( d{q_{m1}} = d{q_{m2}} \)
En régime stationnaire, le débit masse est le même à travers toutes les sections droites d'un même tube de courant.
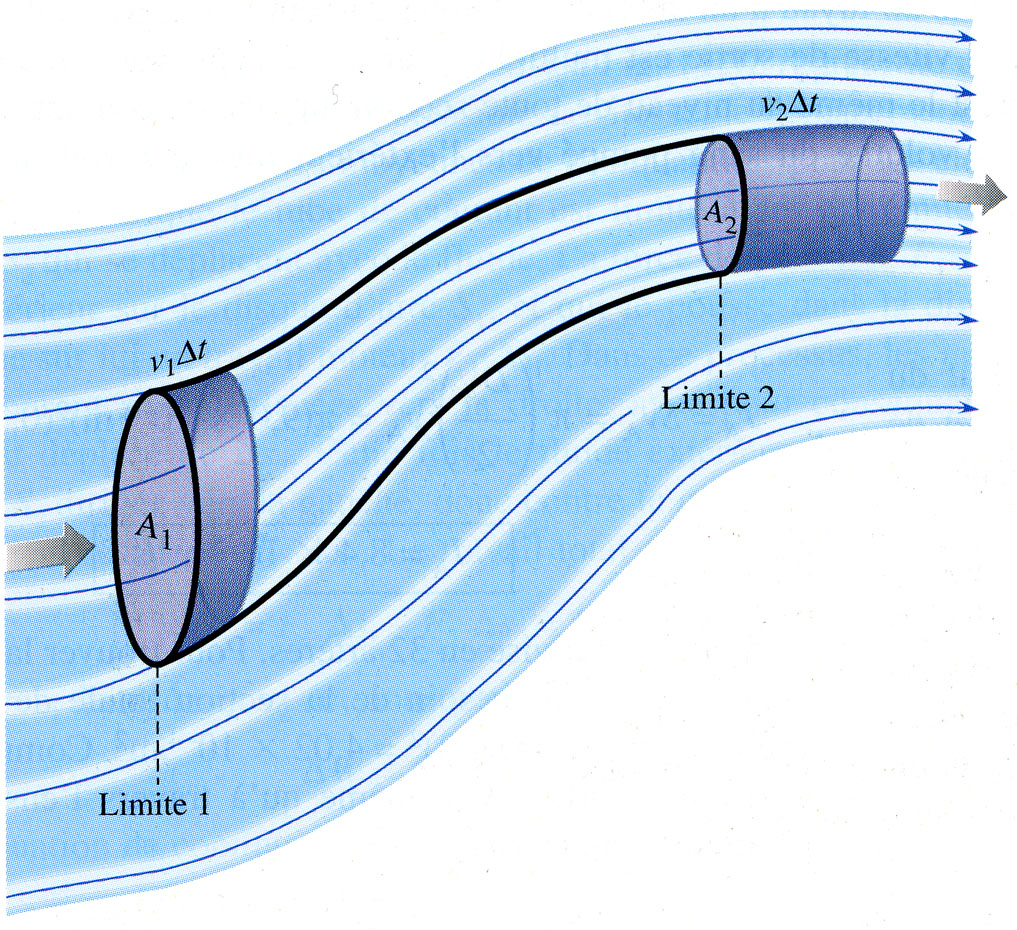
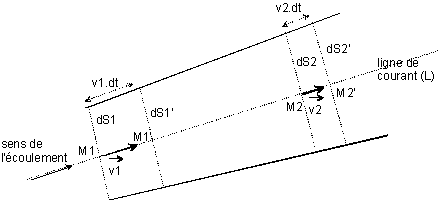
Expression en fonction de la vitesse :
La distance MM' s'écrit v dt en fonction de la vitesse du fluide et donc la relation précédente se met sous la forme : \( d{q_{m1}} = d{q_{m2}} \) soit : \( {\rho _1}{v_1}d{S_1} = {\rho _2}{v_2}d{S_2}\ \) ou \( dq{}_m = \rho {\text{ }}v{\text{ }}dS = Cte\ \)
Pour un écoulement isovolume \( (\rho = C^{te} )\) : \( d{q_{V1}} = d{q_{V2}}\ \) soit : \( {v_1}d{S_1} = {v_2}d{S_2} \) ou \( d{q_V} = v{\text{ }}dS = C^{te} \)
On retrouve évidemment la relation : \( d{q_m} = \rho {\text{ }}d{q_V} \)
Vitesse Moyenne :
En général la vitesse v n'est pas constante sur la section S d'un tube de courant ; on dit qu'il existe un profil de vitesse (forces de frottement). Le débit masse ou le débit volume s'obtient en intégrant le débit élémentaire sur toute la surface S.

Dans une section droite S de la canalisation, on appelle vitesse moyenne vm la vitesse telle que : \( {q_m} = \int_{S} {d{q_m} = Cte} \) ou \( {q_V} = \int_{S} {d{q_V} = Cte} \)
| \( {q_V} = {v_{1moy}} \times {S_1} = {v_{2moy}} \times {S_2} = Cte\ \) |
| \({v_{moy}} = \frac{{{q_V}}}{S} \) |
La vitesse moyenne \( v_{moy} \) apparaît comme la vitesse uniforme à travers la section S qui assurerait le même débit que la répartition réelle des vitesses. Si l'écoulement est isovolume, cette vitesse moyenne est inversement proportionnelle à l'aire de la section droite.





