Généralités
Ce genre de perte est causé par le frottement intérieur qui se produit dans les liquides ; il se rencontre dans les tuyaux lisses aussi bien que dans les tuyaux rugueux.
La rugosité relative d'un tuyau est le rapport de la taille \( k \) des aspérités, rugosités du tuyau sur son diamètre \( D \). Les deux grandeurs étant en m^ètre. Ce nombre est donc sans dimension.
\( \epsilon = \frac{k}{D} \)
Entre deux points séparés par une longueur L, dans un tuyau de diamètre D apparaît une perte de pression \( \Delta p \). exprimée sous la forme suivante :
- Différence de pression (Pa):\( \Delta p = \lambda \frac{{\rho {v^2}}}{2}\frac{L}{D} \)
- Perte de charge exprimée en mètres de colonne de fluide (mCF):\( \Delta h = \lambda \frac{{{v^2}}}{{2g}}\frac{L}{D} \)
- Perte de charge linéique(m/m)(mètre de conduite équivalente): \( J = \frac{{\Delta h}}{L} = \lambda \frac{{{v^2}}}{{2gD}} \)
\( \lambda \) est un coefficient sans dimension appelé coefficient de perte de charge linéaire.
Le calcul des pertes de charge repose entièrement sur la détermination de ce coefficient \( \lambda \).
Cas de l'écoulement laminaire : Re < 2000
Dans ce cas on peut montrer que le coefficient \( \lambda \) est uniquement fonction du nombre de Reynolds Re ; l'état de la surface n'intervient pas et donc \( \lambda \) ne dépend pas de k (hauteur moyenne des aspérités du tuyau), ni de la nature de la tuyauterie.
Le coefficient de perte de charge linéaire vaut alors \( \lambda = \frac{64}{Re} \) avec \( Re = \frac{v D}{\nu } \)
Il est alors immédiat de voir que \( \Delta h \) est proportionnel à la vitesse v et donc au débit q, ainsi qu'à la viscosité cinématique \( \nu \).
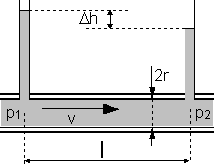
Loi de Poiseuille Pour un écoulement laminaire, dans une conduite cylindrique horizontale, de longueur L, de rayon r (diamètre D), le débit-volume du fluide est donné par : \( q_V = \frac{\pi r^4}{8 \eta L}( p_1 - p_2) = \frac{\pi r^4}{8 \eta L}\Delta p = \frac{\pi D^4}{128 \eta L}\Delta p \)
Cas de l'écoulement turbulent: Re > 3000
Les phénomènes d'écoulement sont beaucoup plus complexes et la détermination du coefficient de perte de charge résulte de mesures expérimentales. C'est ce qui explique la diversité des formules anciennes qui ont été proposées pour sa détermination.
En régime turbulent l'état de la surface devient sensible et son influence est d'autant plus grande que le nombre de Reynolds Re est grand. Tous les travaux ont montré l'influence de la rugosité et on s'est attaché par la suite à chercher la variation du coefficient \( \lambda \) en fonction du nombre de Reynolds Re et de la rugosité k du tuyau.
La formule de Colebrook est actuellement considérée comme celle qui traduit le mieux les phénomènes d'écoulement en régime turbulent. Elle est présentée sous la forme suivante :
\( \frac{1}{\sqrt \lambda } = - 2\log (\frac{k}{3,7 D} + \frac{2,51}{Re \sqrt \lambda}) \)
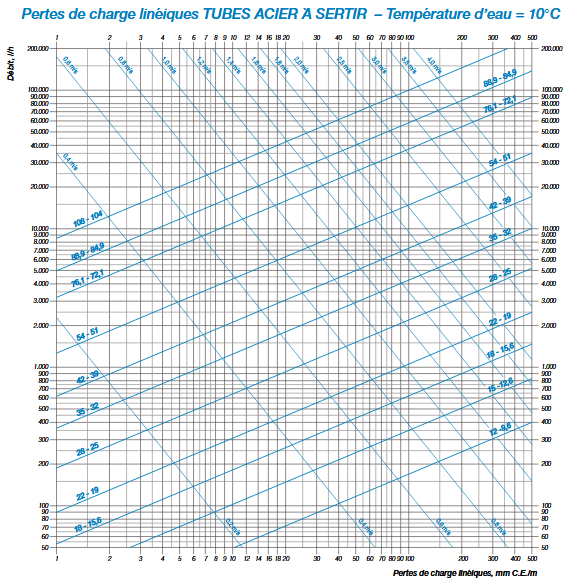
L'utilisation directe de cette formule demanderait, du fait de sa forme implicite, un calcul par approximations successives ; on emploie aussi en pratique des représentations graphiques
Abaques
Exemple