Principe fondamental de la statique des fluides
L'expérience de la plongée sous-marine ou en piscine permet de percevoir cette notion de pression:
- un trajet horizontal sous l'eau (donc à une profondeur constante) ne modifie pas la pression sur les oreilles, pas de gêne particulière est ressentie.
- si l'on s'enfonce, la pression augmente, et appuie sur les tympans générant une douleur. Il faut remonter ou opposer à cette pression externe, une pression interne plus importante par la manœuvre de Valsalva par exemple.
Une mesure avec un capteur de pression confirme cette sensation: si nous plongeons un capteur de pression au sein d'un fluide, nous observons que la pression augmente avec la profondeur (altitude) et ne varie pas dans un plan horizontal.
On peut donc établir une loi qui s'applique sur tout corps immergé dans un fluide: soit un élément de volume de fluide dV se trouvant au point M. Il est soumis à des forces de pression exercées par les parties voisines du fluide.
Si le fluide est en équilibre, les forces de frottement sont nulles. L'élément de volume dV n'est alors soumis, généralement, qu'à son poids et aux forces de pression. La condition d'équilibre de cet élément de fluide permet d'écrire l’équation fondamentale de la « Statique des Fluides ».
Expression différentielle de la relation fondamentale :
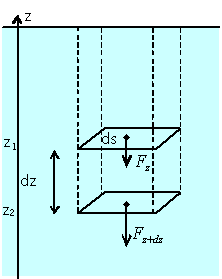
Dans un repère \( (O, \vec i, \vec j, \vec k) \)(l'axe Oz orienté vers le haut) et dans le champ de pesanteur,\( \vec g = -g \cdot \vec k) \), l’expression différentielle de la relation fondamentale de la statique des fluides s'écrit :
\(\frac{{dp}}{{dz}} = - \rho {\text{ }}g\ \) ou
| \( p_2 - p_1 = - {\text{ }}\rho {\text{ }} g {\text{ }}(z_2 - z_1)\ \) |
|
\( dp = - {\text{ }}\rho {\text{ }}g{\text{ }}dz\ \) |
Où \( \rho \) est la masse volumique du fluide considéré en kg/m3.
Pression dans les liquides (http://www.clipedia.be) (21min50)
https://www.youtube.com/watch?v=OHQ5-QWoePA
Le principe de Pascal (http://www.clipedia.be) (25min49)
https://www.youtube.com/watch?v=6f4TFvaBGPQ





