Les filtres sont des quadripôles qui, sur un signal ne vont laisser passer que certaines fréquences.
| Le filtre passe-haut, laisse passer les hautes fréquences au-delà d'une certaine fréquence \( f_0 \) et coupe les fréquence en dessous. | 
|
| Le filtre passe-bas, laisse passer les basses fréquences en dessous d'une certaine fréquence \( f_0 \) et coupe les fréquence au-delà. | 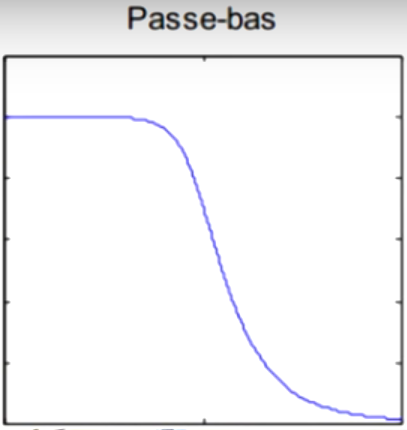
|
| Le filtre passe-bande, laisse passer les fréquences comprises entre \( f_1 \) et \( f_2 \). | 
|
| Le filtre réjecteur de bande, ou coupe bande ne laisse pas laisse passer les fréquences comprises entre \( f_1 \) et \( f_2 \). | 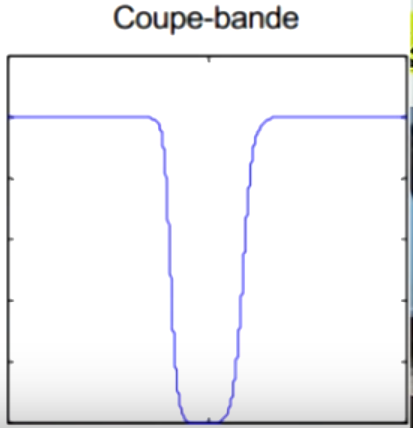
|
Le choix des fréquences se fait en choisissant correctement les éléments qui constituent le filtre.
Un filtre sera caractérisé par la capacité qu'il a à couper brutalement les fréquences qu'il ne doit pas laisser passer: cette capacité dépend de l'ordre du filtre
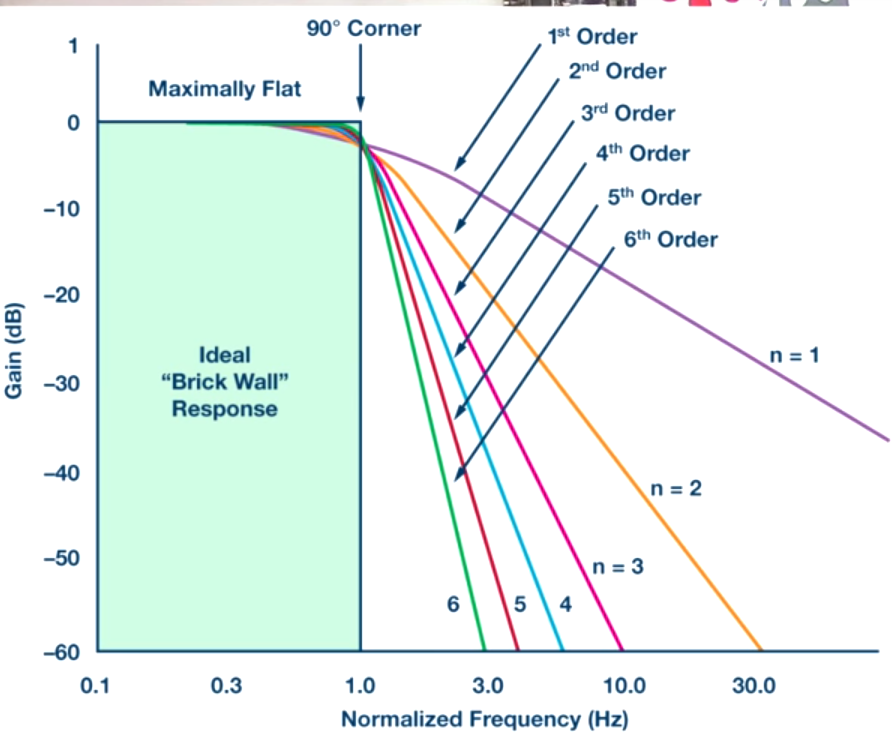
Filtre du premier ordre
Filtre passe bas
La transmittance d’un passe bas est de la forme
| \( T(j\omega ) = \frac{1}{{1 + j\frac{\omega }{{{\omega _0}}}}} \) |
Le module de T est
\( T = \frac{1}{{\sqrt {1 + {{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^2}} }} \)
\( T = \left( {1 + {{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^2}} \right)^{ - \frac{1}{2} } \)
Donc le gain est
\( G = 20 log T = 20 \log \left( {1 + {{\left( {\frac{\omega }{\omega _0}} \right)}^2}} \right)^{-1/2} \)
\( G = - \frac{1}{2}20 \log \left( {1 + {{\left( {\frac{\omega }{\omega _0}} \right)}^2}} \right) = - 10 \log \left( {1 + {{\left( {\frac{\omega }{\omega _0}} \right)}^2}} \right) \)
Et l’argument est \( \arg T = - \arg \left( {1 + j\left( {\frac{\omega }{{{\omega _0}}}} \right)} \right) = - \arctan \left( {\frac{\omega }{{{\omega _0}}}} \right) \)
Il suffit d’étudier ce qui se passe pour diverses valeurs particulières
- Si \( \omega \to 0 \) alors
- \( G = - 10\log \left( {1 + {{\left( {\frac{0}{{{\omega _0}}}} \right)}^2}} \right) = - 10\log 1 = 0 \)
- \( \arg T = - \arctan \left( {\frac{0}{{{\omega _0}}}} \right) = 0 \)
- Si \( \omega \to \infty \) alors
- \( G = - 10\log \left( {1 + {{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^2}} \right) \approx - 10\log {\left( {\frac{\omega }{{{\omega _0}}}} \right)^2} = - 20\log \left( {\frac{\omega }{{{\omega _0}}}} \right) \) ce qui tend vers moins l’infini avec une pente de -20 dB par décade ( -20 dB quand la fréquence est multipliée par 10)
- \( \arg T = - \arg \left( {1 + j\left( {\frac{\omega }{{{\omega _0}}}} \right)} \right) \approx - \arctan \left( {\frac{\infty }{{{\omega _0}}}} \right) = - 90^\circ \)
- Si \( \omega = \omega_0 \) alors
- \( G = - 10\log \left( {1 + {{\left( {\frac{{{\omega _0}}}{{{\omega _0}}}} \right)}^2}} \right) = - 10\log 2 = - 3\,\,dB \)
- \( \arg T = - \arctan \left( {\frac{{{\omega _0}}}{{{\omega _0}}}} \right) = - 45^\circ \)
D’où le tracé du diagramme de Bode:
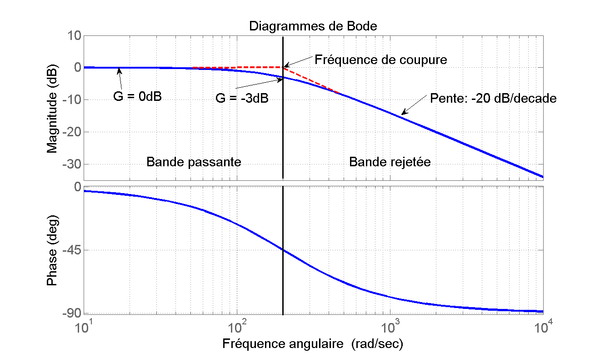
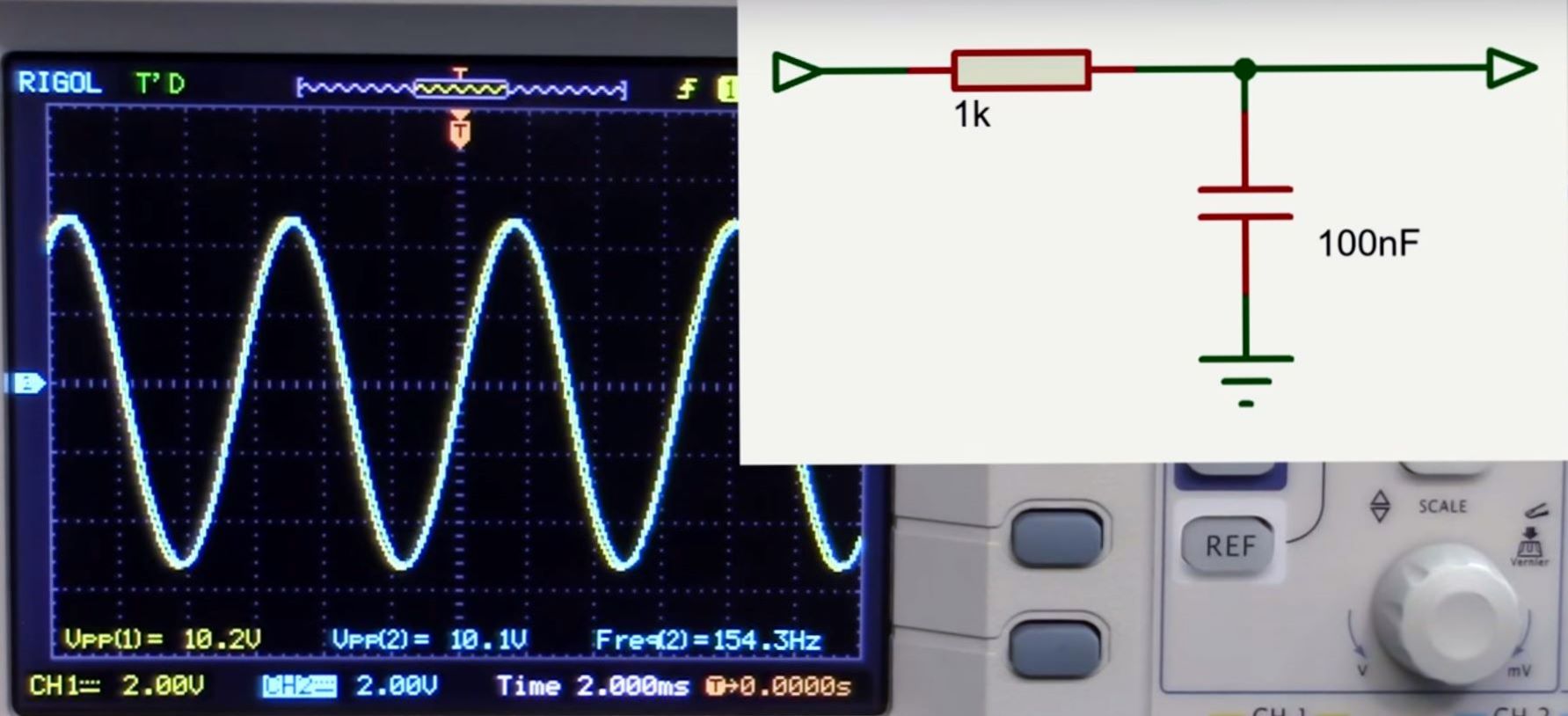
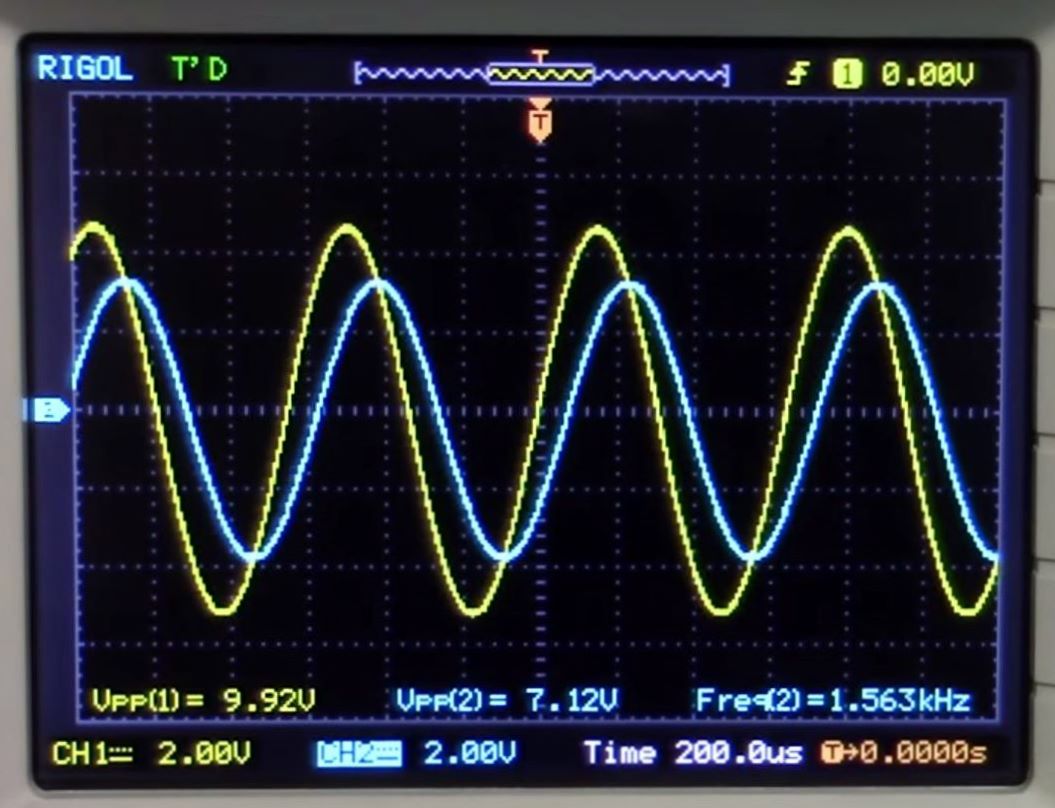

Filtre passe haut
Filtre integrateur
Filtre derivateur
Animation

Vidéos |
| Cours Traitement du signal C05 Filtrage de signaux (60'05") |
| https://youtu.be/n_7LsvHfgek |
| Les filtres analogiques Alain Jeanneaux. La Réussite Académy |
| https://youtu.be/q8ni5GeXc9Y |
| https://youtu.be/X3rfQr4hZCw |
| https://youtu.be/fsrEmi092l4 |






