En monophasé
Pour trouver un modèle série:
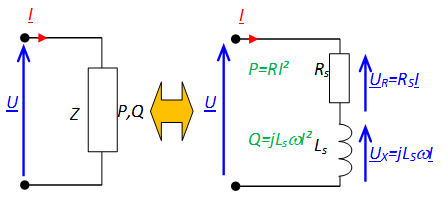
Lorsqu'une installation consomme une puissance active \( P \) et une puissance réactive \( Q \), celle-ci peut être remplacée par une installation composée d'une résistance en série avec une inductance.
Les valeurs de ces éléments sont telles que :
- la résistance consomme l'intégralité de la puissance active d'expression \( P = R \times I^2 \)
- l'inductance consomme l'intégralité de la puissance réactive \( Q = L \omega \times I^2 \)
Donc la résistance équivalente du modèle série vaudra donc:
- \( R = \frac{P}{I^2} \)
- \( L = \frac{Q}{\omega \times I^2} \)
Pour trouver un modèle parallèle :
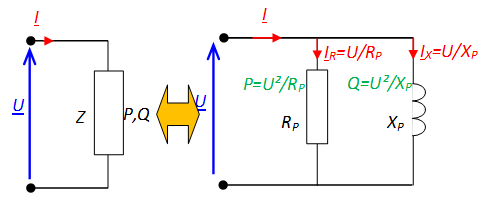
Lorsqu'une installation consomme une puissance active \( P \) et une puissance réactive \( Q \), celle-ci peut être remplacée par une installation composée d'une résistance en parallèle avec une inductance.
Les valeurs de ces éléments sont telles que :
- la résistance consomme l'intégralité de la puissance active d'expression \( P = \frac{U^2}{R} \)
- l'inductance consomme l'intégralité de la puissance réactive \( Q = \frac{U^2}{L \omega} \)
Donc la résistance équivalente du modèle série vaudra donc:
- \( R = \frac{U^2}{P} \)
- \( L = \frac{U^2}{Q \omega} \)
Pour trouver un modèle en triphasé:
Pour trouver un modèle série:
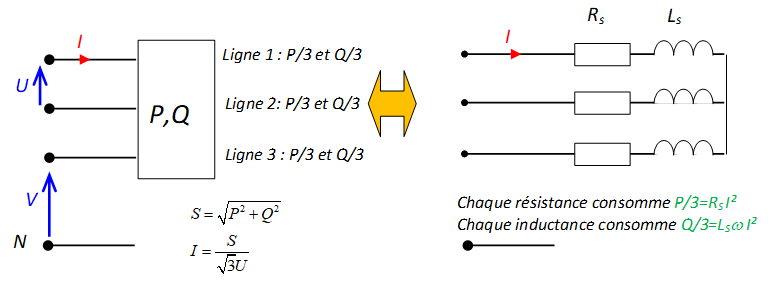
Pour trouver un modèle parallèle:
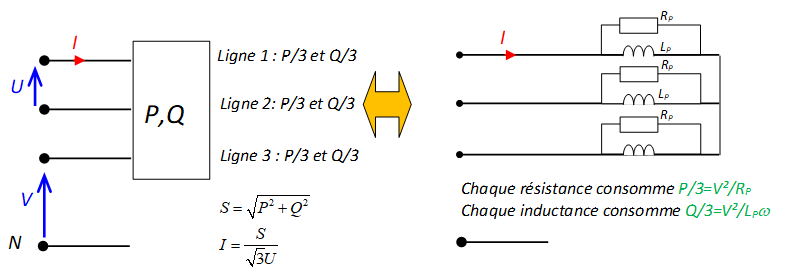
Passage du modèle série au modèle parallèle d'une impédance:
\( R_p = \frac {R_s^2 + X_s^2}{R_s} \) et \( X_p = \frac {R_s^2 + X_s^2}{X_s} \)
Passage du modèle parallèle au modèle série d'une impédance:
\( R_s = \frac {R_p \times X_p^2}{R_p^2 + X_p^2} \) et \( X_s = \frac {R_p^2 \times X_p}{R_p^2 + X_p^2} \)





