En monophasé
Dans un circuit alimenté sous une tension sinusoïdale de fréquence constante, la puissance active totale :\( P_{tot} \) dissipée dans un groupement de dipôles est égale à la somme des puissances actives dissipées par chaque dipôle.
Il en est de même pour la puissance réactive : \( Q_{tot} \).
La connaissance de la puissance active totale et de la puissance réactive totale permet de connaître la puissance apparente totale \( S_{tot} \) de l'installation et d'en déduire le courant consommé .
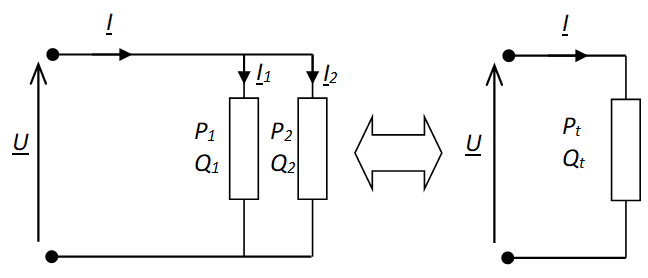 Charges en parallèle 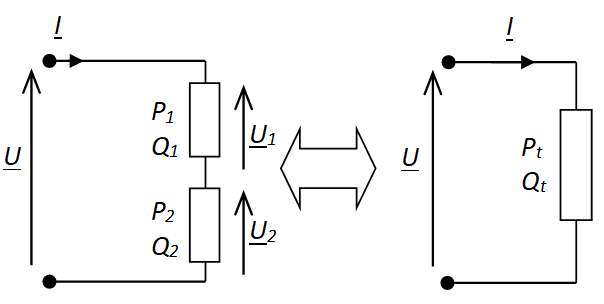 Charges en série |
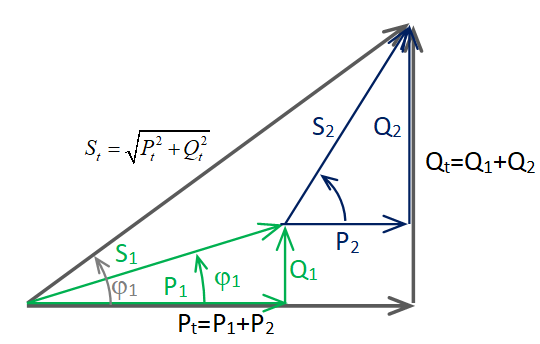 |
Ceci peut se résumer par :
| \( P_{tot} = P_1 + P_2 + ... = \sum\limits_{i = 1}^{i = n} {P_i}\) |
| \( Q_{tot} = Q_1 + Q_2 + ... = \sum\limits_{i = 1}^{i = n} {Q_i}\) |
La puissance apparente \( S_{tot} \) de l’ensemble n’est pas la somme des puissances apparentes.
On calcule d’abord \( P_{tot} = \sum\limits_{i = 1}^{i = n} {P_i} \) et \( Q_{tot} = \sum\limits_{i = 1}^{i = n} {Q_i} \) on déduit la puissance apparente de l’ensemble avec le triangle des puissances: \( S = \sqrt {P_{tot}^2 + Q_{tot}^2} \)
En monophasé: chaque dipôle est alimenté par une tension simple V
| \( P_{tot} = \sum\limits_{i = 1}^{i = n} {P_i} = VI cos \varphi \) |
| \( Q_{tot} = \sum\limits_{i = 1}^{i = n} {Q_i} = VI sin \varphi \) |
On détermine ensuite la puissance apparente qui dépend des puissances active et réactive totales:
| \( S_{tot} = \sqrt{P_{tot}^2 +Q_{tot}^2} \) |
On détermine ensuite à l'aide de la définition de la puissance apparente en monophasé \( S=V \times I \) le courant consommé par l'ensemble de l'installation:
| \( \Rightarrow I = \frac{S}{V} \) |
Le facteur de puissance de l'installation est donné par
| \( f_P = \frac{P_{tot}}{S_{tot}} \) |





