En régime sinusoïdal

Par définition le facteur de puissance d'un circuit en régime quelconque (sinusoïdal ou non) est le rapport entre la puissance active et la puissance apparente.
On le note k ou fp :
| \( k = f_p = \frac{P}{S} \) |
Remarque : le facteur de puissance d'une installation est compris entre 0 et 1
- Uniquement en régime sinusoïdal: \( k = f_p = \frac{P}{S} =cos \varphi \)
Valeurs courantes du facteur de puissance
Préconisation d'EDF
En France, EDF incite (pour les abonnés des tarifs jaune ou vert) un facteur de puissance minimum de 0.93 .
- Donc \( cos \varphi > 0.93 \)
- Donc par un angle de déphasage entre le courant et la tension \( \varphi < 21,8° \)
- soit \( tan \varphi < 0.4 \).
- Ceci peut aussi se traduire par une incitation à consommer moins de 40% de son énergie active en énergie réactive.
Ce choix est dicté par une volonté que la puissance qui transite dans les câbles de distribution soit principalement de la puissance active , et donc utile, et pas de la puissance réactive qui participe à l'augmentation du courant et donc des pertes par échauffement dans les câbles.
Prenons l'exemple de deux installations qui consommeraient 1000 W sous U = 220 V avec comme facteur de puissance \( cos \varphi_1 =1 \) et \( cos \varphi_2 = 0.5 \).
Les courants en lignes sont respectivement: \( I_1= \frac{P}{U \times cos \varphi_1}= 4.54 A \) et \( I_2 = \frac{P}{U \times cos \varphi_2} = 9.1 A \)
Or les pertes en lignes sont proportionnelles à \( I^2 \) car égales à \( P_{pertes} = R_{ligne} \times I^2 \).
Le courant de l'installation 2 est double de celui dans l'installation 1. Les pertes en lignes seront donc 4 fois plus grandes dans le cas de l'installation 2.
Ceci est la raison pour laquelle EDF exige un facteur de puissance minimum et donc de compenser l'énergie réactive.
En régime non-sinusoïdal
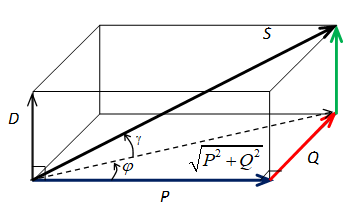
- le facteur de puissance est toujours
| \( k = f_p = \frac{P}{S} = \frac{P}{\sqrt{P^2+Q^2+D^2}} \) |
- le \( cos \varphi \) est aussi nommé Déplacement du Facteur de Puissance
| \( cos \varphi = DFP = \frac{P}{\sqrt{P^2+Q^2}} \) |