Définition
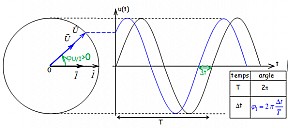
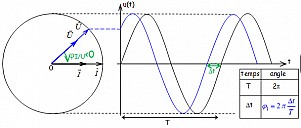
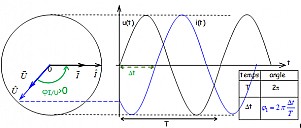
On considère deux grandeurs sinusoïdales de même fréquence:
- \( i(t)=I\sqrt{2} sin(\omega t + \varphi_i) \)
- \( u(t)=U\sqrt{2} sin(\omega t + \varphi_u) \)
Les deux vecteurs \( \vec U \) et \( \vec I \) tournent à la même vitesse.
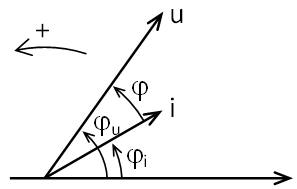
On appelle \( \varphi \) le déphasage de u tension par rapport à i intensité \( \varphi = \varphi_{u/i} = \varphi_{u} -\varphi_{i} \).
Valeurs particulières
| \( \varphi = 0 \): Les deux tensions sont en phases : \( \varphi_i = \varphi_u \) |  |
| \( \varphi = \pi \): Les deux tensions sont en opposition de phases : \( \varphi_u = \varphi_i + \pi\) |  |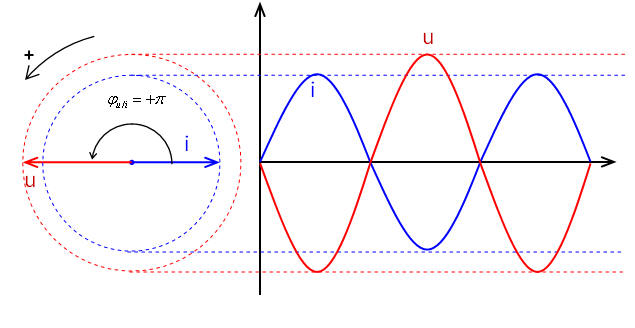
| \( \varphi = +\pi / 2 \): u est en quadrature avance sur i : \( \varphi_u = \varphi_i +\pi / 2\) |  |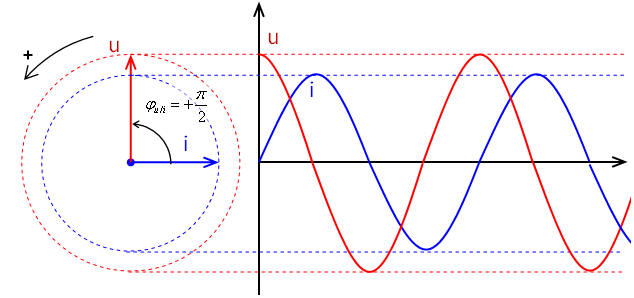
| \( \varphi = -\pi / 2 \): u est en quadrature retardsur i : \( \varphi_u = \varphi_i -\pi / 2\) |  |
Mesure
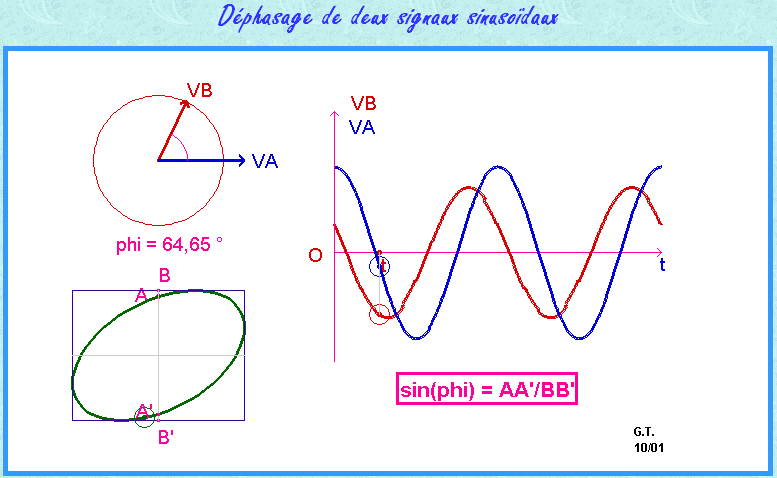
On peut remarquer qu'il existe bien une proportionnalité entre
- le temps \( \Delta t\) mis par une flèche pour tourner d'un angle \( \varphi \).
- le temps \( T \) mis par la flèche pour faire un tour soit \( 2 \pi \) ou 360°
Une relation classique du déphasage est donc
| \( \varphi = \frac{360 \times \Delta t}{T}\) |
avec
- \( \varphi \) l'angle en degrés
- \( \Delta t\) le temps séparant le passage par 0 et dans le même sens de chacune des courbes
- \( T \) la période des sinusoïdes
la même expression avec l'angle en radians
| \( \varphi = \frac{2 \pi \times \Delta t}{T}\) |
Signe de \( \varphi \)
Le signe de \( \varphi \) dépend de ce qui est considéré. Est-ce \( \varphi_{U/I} \) ou \( \varphi_{I/U} \)?
- \( \varphi_{U/I} \) doit se lire angle \( \varphi \) de U par rapport à I. Donc I sert de référence (d'origine des phases).
| donc si U est en avance sur le cercle trigonométrique (à t=0 U est alors >0 si i passe par 0) alors \( \varphi_{U/I} > 0 \) | 
|
| donc si U est en retard sur le cercle trigonométrique (à t=0 U est alors <0 si i passe par 0) alors \( \varphi_{U/I} < 0 \) | 
|
- \( \varphi_{I/U} \) doit se lire angle \( \varphi \) de I par rapport à U. Donc U sert de référence (d'origine des phases).
| donc si I est en avance sur le cercle trigonométrique (à t=0 I est alors >0 si u passe par 0) alors \( \varphi_{I/U} > 0 \) | 
|
| donc si I est en retard sur le cercle trigonométrique (à t=0 I est alors <0 si u passe par 0) alors \( \varphi_{I/U} < 0 \) | 
|
Applets flash pour visualiser et s'entrainer
 |  |  |
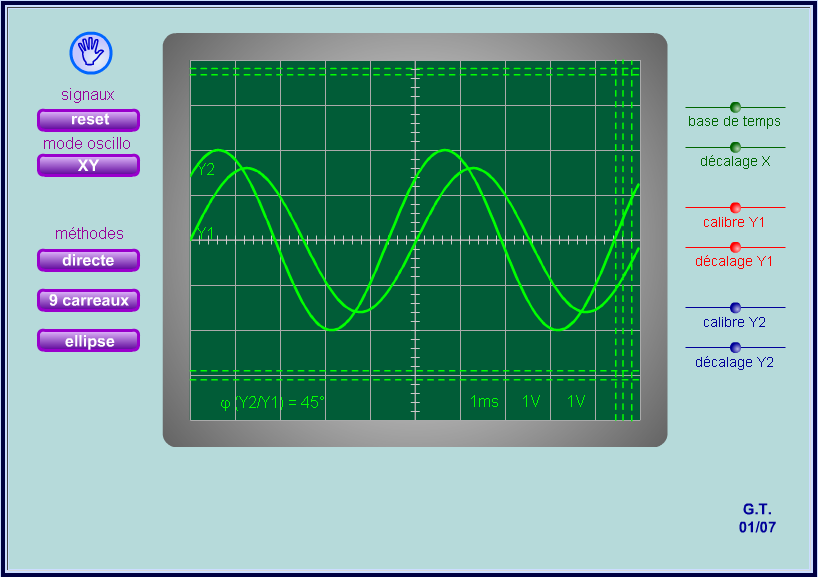Mesurer un déphasage
| Chapitre 2.2 Le monophasé - Comment déterminer un déphasage (Ismail SADKY) (3'01) |
| https://youtu.be/Ej-GlD6TM_4?start=7&rel=0%% |
| Principe de Mesure Déphasage (Franck Corbin) (5'08") |
| https://youtu.be/84zuX5CEeGo?rel=0 |
