Poids d’un objet :
Le poids d’un objet est dû à l’attraction terrestre.
Cette force verticale est orientée vers le bas .
Elle s’exerce sur le centre de gravité de l’objet :
| \( \vec P = m\vec g \) |
avec \( g=9,81 N \cdot kg^{-1} \) à la surface de la terre. |
La constante de gravitation g est liée aux masses en présences et à la distance les séparant:
\( P = G \frac{m_1 \times m_2}{r^2} \) où \( g = G \frac{m_1}{r^2}\)
- \( P \) le poids en \( N \)
- \( G \) la constante de gravitation \( G =6,67 \cdot 10^{-11} m^{-3} \cdot kg^{-1} \cdot s^{-2}\)
- \( g \) accélération de la pesanteur en \( N/kg \) ou \( m \cdot s^{-2} \) de l'astre de masse \( m_1 \).
- \( r \) la distance séparant les deux centre de gravité en \( m \).
| Astre | Masse | Rayon |
|---|---|---|
| Mars | \( 6.40 10^{23} kg \) | 3 390 km |
| Terre | \( 5.98 10^{24} kg \) | 6 380 km |
| Lune | \( 7.342 10^{22} kg \) | 3 474 km |
| Jupiter | \( 1,898 10^{27} kg \) | 69 911 km |
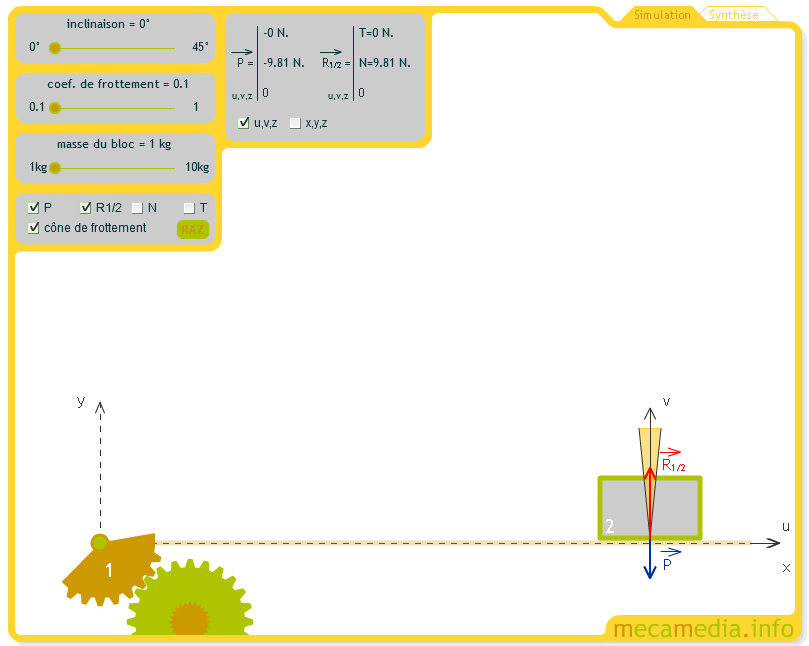
Réaction d’un plan sur un solide :
C’est une force répartie en surface qui s’oppose à la pénétration du solide dans le plan considéré. Elle peut-être décomposée en deux composante: une composante normale (perpendiculaire) au plan et une composante tangentielle (parallèle) au plan. \( \vec R = {\vec R_N} + {\vec R_T} \).
- \( {\vec R_N} \) est la composante normale de la réaction ou réaction normale. Elle est normale au plan. Les actions de contact entre deux solides sont répulsives. La valeur de \( R_N \) est telle que la réaction normale s'oppose à la composante normale au plan du poids \( P_N \)
\( R_N = P_N \).
- \( {\vec R_T} \) est la composante tangentielle de la réaction ou réaction tangentielle ou vecteur « force de frottement ». Par sa direction et son sens, la force de frottement s’oppose au glissement du solide.
|
à plat le solide ne s'enfonce pas donc \( R=P \) |
en pente: tant que la force de frottement (ou réaction tangentielle) \( R_T \) est égale à la composante tangentielle du poids \( P_T \) le solide ne bouge pas |
en pente: si la composante tangentielle du poids \( P_T \) devient supérieure à la force de frottement alors de part la Relation Fondamentale de la Dynamique le solide glisser et accélérer sa descente. |
Les forces de frottement des solides:
Définition
- Si deux surfaces en contact se déplacent ou glissent l’une par rapport à l’autre, on dit qu’il y a frottement.
- Quand ces surfaces tendent à glisser mais ne se déplacent pas, on parle d’adhérence.
Quand la force devient supérieure à \( {F_{\lim }} = {\mu _S}.R \) , le colis glisse sur le sol. Ce mouvement continuera à vitesse uniforme si on applique \( F’=\mu \cdot R ( <{\mu _S}.R \), c’est à dire <Flim).
Il faut F>Flim pour mettre l’objet en mouvement mais une force inférieure sera suffisante pour maintenir le mouvement. La force \( \vec f \) s’opposant au mouvement est telle que \( f = \mu.R \) avec \(\mu\) coefficient de frottement dynamique.
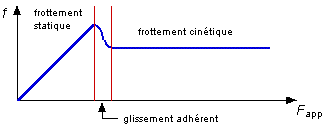
Exemples : (donnés à titre indicatifs, de grosses variations peuvent apparaitre)
- Pneu de voiture sur route :\( {\mu _S}=0,8 \) ; \( \mu=0.6 \) ; \( \mu=0.1 à 0.3 \) sur sol mouillé.
- Acier sur acier : \( {\mu _S}=0,18 \) ; lubrifié: \( {\mu _S}=0,12 \) ; \( \mu=0.15 \) ; lubrifié : \( \mu=0.09 \)
Le coefficient de frottement dépend essentiellement de la nature des matériaux en contact et de la qualité des surfaces en contact. Il est indépendant des efforts exercés ainsi que de l’étendue des surfaces en contact.
Dans les cas abordés, la différence entre force d'adhérence et de frottement seront négligées et considérées comme égales
Si on exerce une poussée latérale \( \vec F \) passant par le centre de gravité G, deux cas sont possibles :
- Il n’y a pas de mouvement, le colis est en équilibre. Il existe (d’après le principe fondamental de la dynamique) une force d’adhérence \( {\vec f} \) égale à \( \vec F \) et de sens opposé.\( {\vec f} \) s’oppose au déplacement éventuel de l’objet vers la droite (dans ce cas). Si la force \( \vec F \) augmente la force de frottement va augmenter elle aussi. La résultante des forces de réactions \( \vec f + \vec R\) présente un angle \( %alpha_1 \) avec la verticale qui augmente lui aussi avec la force. Lorsque la force \( {\vec F} \) augmente la force de frottement \( {\vec f} \) augmente aussi et l'angle \( %alpha \) aussi jusqu'à un angle limite \( %alpha_lim \)
- Si \( \vec F \) devient suffisante, \( \vec F > \vec F_{\lim } \) , l’objet se met à glisser dans le même sens que \( \vec F \). La résultante \( \vec f + \vec R\) présente le même angle \( %alpha_lim \) trouvé au moment de l'amorce du glissement. Le vecteur \( \vec f \) reste alors constant, si la force de traction \( \vec F \) reste constante et supérieure à la force de frottement, le solide se déplace alors à accélération constante déterminée par le principe fondamental de la dynamique.
Relation
La valeur de cet angle limite permet de déterminer la force de frottement.
De part la construction graphique, la force de frottement est donnée par \( f = tan (\alpha_{\lim }) . R \)
| \( f = {\mu _S}.R = tan (\alpha_{\lim }) . R \) |
On note coefficient de frottement statique ou coefficient d’adhérence \( {\mu _S} = \frac{{{F_{\lim }}}}{R} = \frac{{{f_{a\lim }}}}{R} \).

Où \( {\mu _S} = \tan {\alpha _{\lim }} \) avec \( \alpha _{\lim } \) angle de frottement statique.
Animations :
Les forces de frottement d'un solide dans un fluide:
Expression de la trainée:
La force de frottement d'un objet sur un fluide est aussi appelée trainée.
Elle dépend
- de la masse volumique \( \rho \) du fluide dans lequel le solide se déplace en \( kg/m^3 \)
- de la vitesse du solide \( v \) en \( m/s \)
- de la surface faisant face au déplacement \( S \) en \( m^2 \)
- d'un coefficient de forme traduisant le pouvoir de pénétration du solide appelé coefficient de trainée\( C_x \)
La force de frottement prend donc l'expression:
| \( R = \frac{1}{2} C_x \rho S v^2\) |
Vitesse atteinte par un objet en chute libre:
La RFD appliquée à un objet en chute libre s'écrit ainsi:
\( m \cdot a = m \cdot g - \frac{1}{2} C_x \rho S v^2\)
soit \( m \cdot \frac{dv}{dt} = m \cdot g - \frac{1}{2} C_x \rho S v^2\)
cette équation différentielle est telle que \( V_{max} = \sqrt{\frac{2 m g}{C_x \rho g}} \)
L'équation différentielle du type \( \frac{dy}{dt}=1-y^2 \) a pour solution \( y=tanh(t) \)
donc la solution de cette équation est \( v(t) = V_{max} tanh\frac{t}{T} \)
Liens
Poussée d’Archimède :
Enoncé
C’est la force unique équivalente aux forces pressantes qui s’exerce sur tout objet immergé dans un fluide. Elle est de direction verticale, de bas en haut et de valeur égale au poids du fluide déplacé. Elle est appliquée au centre de poussée ou centre de gravité du fluide déplacé.
\( {\vec P_a} = - {\rho _o}V\vec g \)
- Pa en N ;
- \( \rho_0 \) masse volumique du fluide en kg/m3,
- V volume du fluide déplacé en m3 ;
- g accélération de la pesanteur en N/kg.(g=9,81 N.kg-1 ou m.s-2 en France).
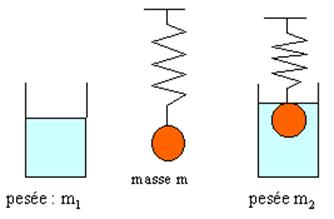
La différence d'élongation du ressort correspond à la poussée d'Archimède, qui est égale au volume de la sphère multiplié par la masse volumique de l'eau fois la gravitation.
| Poussée d'archimède dans du SF6 30" | Clipédia la poussée d'Archimède 17'14" | Eureka, La poussée d'Archimède 6'13" |
Exercices
On place un matelas pneumatique gonflé sur l’eau d’une piscine.
Qu’est-ce qui fera monter le plus le niveau de l’eau :
Lancer une pièce de 1 euro dans l’eau ? OU Lancer une pièce de 1 euro sur le matelas ?
https://www.enigme-facile.fr/enigme-piece-matelas-piscine-4557
Tension exercée par un ressort :
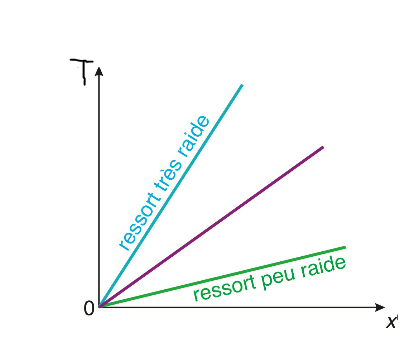
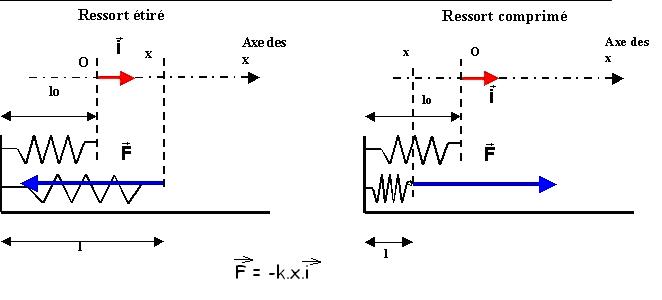
Le vecteur force de tension exercé par un ressort en A est dirigé suivant l’axe du ressort, orienté soit vers l’extérieur du système (ressort étiré) soit vers l’intérieur du système (ressort comprimé), de valeur d’autant plus grande que le ressort est étiré (ou comprimé):
| \( T = k.\left| {\Delta l} \right| \) |
- T valeur de la tension en N
- \( \left| {\Delta l} \right| \) allongement ou compression en m
- k constante de raideur en N/m.
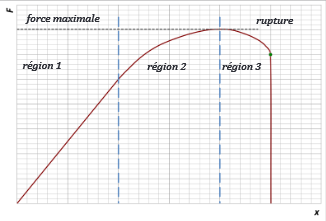
Le ressort subit une déformation et revient à sa position initiale au repos: on parle alors de déformation élastique si le corps reprend sa forme initiale lorsque la force n’agit plus sur le corps.
On parle de déformation plastique si le corps ne reprend plus sa forme initiale lorsque la force n’agit plus sur le corps.
Lorsque l'on utilise une ressort, dynamomètre ou autre objet basé sur sa déformation il faut toujours veiller à ne pas dépasser sa limite d'élasticité et donc rester dans sa plage d'utilisation.
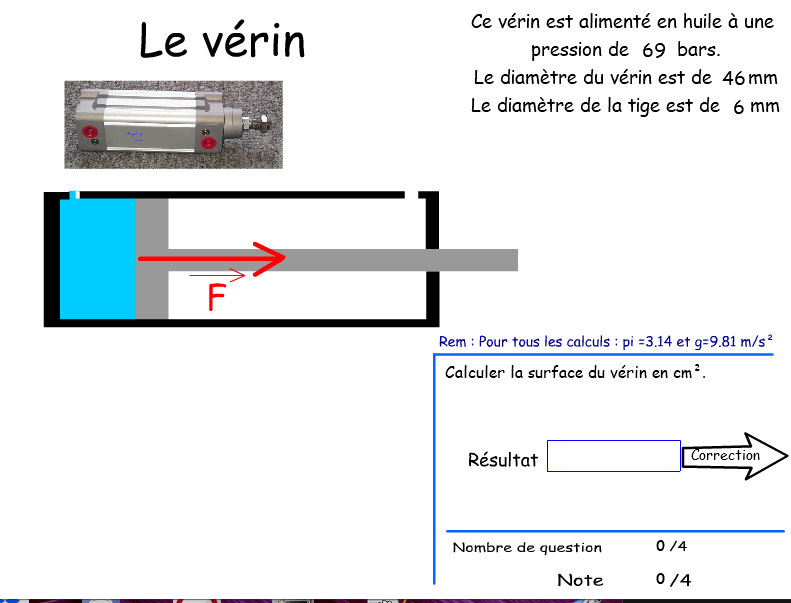
La force d'un vérin
La force développée par un vérin dépend de la pression du fluide exerçant la contrainte et de la section du vérin sur laquelle s'applique la pression.
| \( F={P} \times {S} \) |