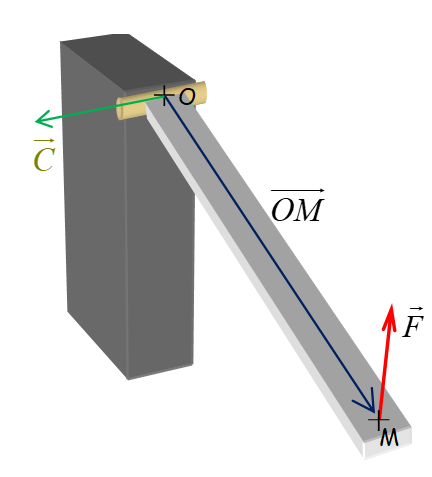
Le moment d'une force est un couple de force où la deuxième force est constituée par la force de réaction de l’axe.
Si la force et le bras de levier sont perpendiculaires on retrouve
\( C = OM \cdot F \)
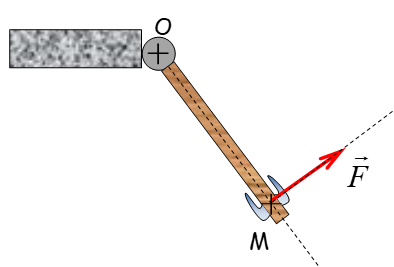
Si on considère la force exercée sur la poignée d'une porte d'orientation quelconque, le couple ainsi créé dépend de l'orientation de la force par rapport à la porte.

\( C = OM \cdot F \cdot sin \alpha \)
Une prise en compte plus rigoureuse dans son écriture mathématique placera le couple comme un vecteur orienté dans l'espace qui permettra ainsi de comptabiliser le sens de rotation généré par le couple.
Le vecteur couple \( \vec C \) est un vecteur correspondant au produit vectoriel de \( \overrightarrow {OM} \) par \( \vec F \). Ce qui se note:
\( \vec C = \overrightarrow {OM} \wedge \vec F \)
La norme de ce vecteur est donnée par
| \( C = OM \cdot F \cdot \sin \alpha \) |
ou si l'on rassemble OM et \( \sin \alpha \) : \( C = d \cdot F \)
l'orientation de ce vecteur couple est donné par la règle des 3 doigts de la main droite
avec
- \( OM \) (distance entre le point d'application de la force et l'axe de rotation) en \( m \)
- ou \( r \) (en \( m \))
- \( F \) en \( N \).
- \( C \) en \( N.m \).