Définition du moment d'inertie
Le moment d’inertie quantifie la résistance d’un corps à la mise en rotation, comme la masse représente la résistance du corps à une mise en mouvement linéaire.
Plus la matière est éloignée de l’axe de rotation, plus la résistance au mouvement est importante.
En effet, il faut communiquer une vitesse angulaire \( \Omega \) à tous les points du système. \( v = r \cdot \Omega\). La vitesse linéaire à donner aux éléments dépend de leur distance à l’axe. Plus la distance est grande, plus cette vitesse est importante, plus il faudra d’énergie pour mettre le système en mouvement.
Chaque élément de masse \( m_i \) du solide, placé à une distance \( r_i \) de l'axe de rotation possède un moment d'inertie \( J_i = m_i r_i^2 \). Il faut donc ajouter tous les éléments de masse pour connaître le moment d'inertie total du solide.
\( J = \sum\limits_i {{m_i}r_i^2} \)
Additions de moments d'inertie
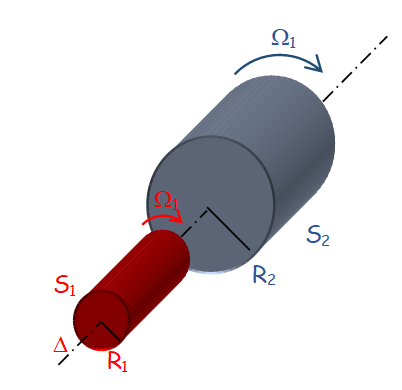
Si plusieurs pièces sont en rotation sur le même arbre, leurs moments d'inertie s'additionnent.
| \( J_{total} = \sum J_i \) |
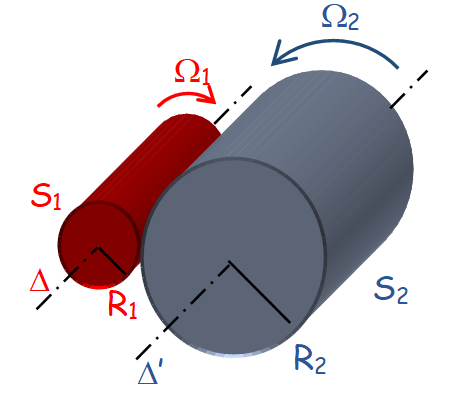
Si un arbre moteur entraîne plusieurs pièces en rotation par l'intermédiaire de divers accouplement les moments s'additionnent, mais pondérés du rapport de réduction au carré existant entre l'arbre sur lequel on veut connaître le moment d'inertie et les diverses pièces en rotation.
| \( {J_t} = {J_1} + {r^2}{J_2} \) |
Le rapport de réduction des vitesses \( r = \frac{{{\Omega _2}}}{{{\Omega _1}}} = \frac{{{R_1}}}{{{R_2}}} \)
Si l’on veut connaître le moment d’inertie totale du système du point de vue de l’axe de rotation \( \Delta \).
Le solide \( S_2 \) offrant une inertie supplémentaire, comment s’ajoutent les moments d’inertie dans ce cas ?
Une manière simple de résoudre le problème est de considérer les énergies de chacun des solides.
- Le solide \( S_1 \) tourne à \( \Omega_1 \) et possède donc une énergie \( {E_{C1}} = \frac{1}{2}{J_1} \cdot \Omega _1^2 \)
- Le solide \( S_2 \) tourne à \( \Omega_2 \) et possède donc une énergie \( {E_{C2}} = \frac{1}{2}{J_2} \cdot \Omega _2^2 \)
- L’énergie totale est donc \( {E_C} = {E_{C2}} + {E_{C1}} = \frac{1}{2}{J_1} \cdot \Omega _1^2 + \frac{1}{2}{J_2} \cdot \Omega _2^2 \)
Et si l’on exprime cette énergie qu’en fonction de la vitesse qui nous intéresse, soit \( \Omega_1 \), alors :
\( {E_C} = \frac{1}{2}{J_1} \cdot \Omega _1^2 + \frac{1}{2}{J_2} \cdot {\left( {r \cdot {\Omega _1}} \right)^2} = \frac{1}{2}\left( {{J_1} + {r^2}{J_2}} \right)\Omega _1^2 \)
Le moment d’inertie de l’ensemble est donc
| \( {J_t} = {J_1} + {r^2}{J_2} \) |
| le moment d'inertie (1 : Le mouvement d'un anneau et d'un cylindre) (2'33") |
| https://youtu.be/if-YOfs2h_4 |
| La dynamique de la rotation et le moment d'inertie clipedia (54'44") |
| https://www.youtube.com/watch?v=i0dTMI1N9Co |
| Xenius: volant d'inertie (25"45') |
| https://youtu.be/cfRL96ZkBkg |
| TP de Physique 3 : Le moment cinétique (4 : l'hélicoptère) (1'51") |
| https://youtu.be/LBgr5MkcRuE |





