Impédance d'un dipôle

Loi d'Ohm généralisée:

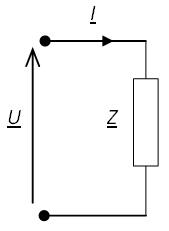
La notion d'impédance décrit de façon plus générale et plus précise ce que l'on a approché avec la notion de résistance et sa loi d'Ohm.

L'impédance traduit le rapport qui existe entre la tension et le courant, mais aussi le déphasage qui existe entre cette tension et ce courant.

L'impédance est définie par le rapport de la tension complexe sur le courant complexe.

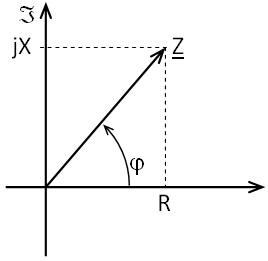
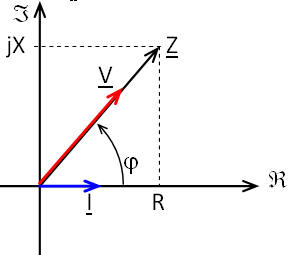
L'impédance est donc définie par $\underline{Z}=\left[ {Z;\varphi } \right]$ avec

• le module de l'impédance $Z = \frac{U}{I}$ en Ohm ($\Omega$), qui est le rapport de la tension sur le courant traversant le dipôle:
• la phase de Z, aussi appelée argument de Z: $arg \underline{Z} = \varphi = {\varphi _u} - {\varphi _i}$, qui est le déphasage entre la tension et le courant.

L'impédance vue sous forme polaire peut aussi être vue sous forme cartésienne en se rappelant des formules de trigonométrie:

• en une partie réelle que l'on appellera résistance R qui constitue la partie résistive du dipôle Z,

• et en une partie imaginaire que l'on appellera réactance X qui constitue la partie réactive du dipôle Z,

Impédances des dipôles simples

• La résistance
• La bobine
• Le condensateur

Vidéos

Bilan des impédances des dipôles simples

Dipôle	Résistance	Bobine	Condensateur
Schéma
Loi d'Ohm généralisée	$u_R = R \times i$	$u_L = L \times \frac{{di}} {{dt}}$	$i = C \times \frac{{du_C}} {{dt}}$
Association série	$R_{eq} = \sum\limits_{i = 1}^n {R_i }$	$L_{eq} = \sum\limits_{i = 1}^n {L_i }$	$\frac{1}{{C_{eq} }} = \sum\limits_{i = 1}^n {\frac{1}{{C_i }}}$
Association parallèle	$\frac{1}{{R_{eq} }} = \sum\limits_{i = 1}^n {\frac{1}{{R_i }}}$	$\frac{1}{{L_{eq} }} = \sum\limits_{i = 1}^n {\frac{1}{{L_i }}}$	$C_{eq} = \sum_{i = 1}^n {C_i }$
Impédance en sinusoïdal	$\underline{Z}=R=\left[{R;0}\right]$	$\underline{Z}_L = jL\omega = \left[ {L\omega ;\frac{\pi }{2}} \right]$	$\underline{Z}_C = \frac{1}{jC\omega} = \left[ {\frac{{1}} {{jC\omega}} ; -\frac{\pi }{2}} \right]$
Puissance active $P$ en sinusoïdal	$P = R \times I^2 = \frac{U^2}{R}$	$P = 0$	$P = 0$
Puissance réactive $Q$ en sinusoïdal	$Q = 0$	$Q = L \omega \times I^2 = \frac{U^2}{L \omega}$	$Q = C \omega \times U^2 = \frac{I^2}{C \omega}$
Modèle plus réaliste

QCM

• QCM Fresnel http://fabrice.sincere.free.fr/qcm/qcm.php?nom=qcm_fresnel

• QCM impédance : http://fabrice.sincere.free.fr/qcm/qcm.php?nom=qcm_impedance
• QCM Circuit linéaire en régime sinusoïdal http://fabrice.sincere.free.fr/qcm/qcm.php?nom=qcm_sinus